Question

已知f(x)=

2

sin(2x-

π

4

)，x ∈[

π

4

，

5π

4

]
（Ⅰ）用五点作图法作出f（x）的图象，并指出函数的单调区间和值域；
（Ⅱ）若f（x）=a有两个不同的实数根，请你求出这两根之和．

Answer 1

分析：（Ⅰ）令2x-

π

4

分别等于

π

4

，

π

2

，π，

3π

2

，2π，求出五个对应的（x，y）值，在坐标系中描出这五个点，再用平滑的曲线连接，即得函数在一个周期上的图象．
（Ⅱ）通过a的值使得方程有两个实数根，利用函数的对称性，求出两个根之和即可．

解答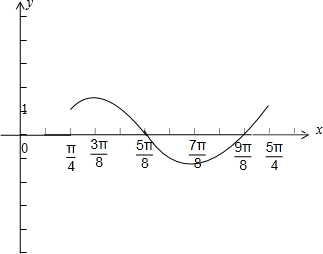：解：（1）列表：

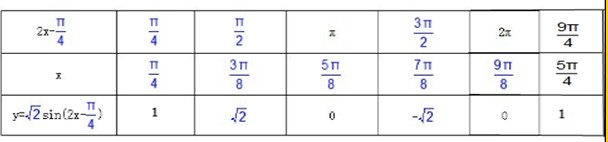
描点作图：
 由表知，函数单调增区间是[

π

4

，

3π

8

]，[

7π

8

，

5π

4

]．单调减区间[

3π

8

，

7π

8

]，函数的值域为[-

2

，

2

]
（Ⅱ）由函数的图象可知，当a∈[1，

2

）时，两个根关于x=

3π

8

对称，所以两根和为：

3π

4

．
当a∈(-

2

，-1]时，两个根关于x=

7π

8

对称，所以两根和为：

7π

4

．

点评：本题考查用五点法作y=Asin（ωx+∅）的图象，求出图象上五个关键点的坐标，考查函数的图象的应用．