题目内容
 已知f(x)=2sin(2x-
已知f(x)=2sin(2x-| π |
| 3 |
(1)求f(x)的单调增区间;
(2)求f(x)图象的对称轴的方程和对称中心的坐标;(3)在给出的直角坐标系中,请画出f(x)在区间[-
| π |
| 2 |
| π |
| 2 |
分析:(1)利用正弦函数的单调增区间直接求解f(x)的单调增区间;
(2)通过正弦函数的对称轴方程和对称中心的坐标,直接求f(x)图象的对称轴的方程和对称中心的坐标;
(3)通过列表,描点,连线在给出的直角坐标系中,请画出f(x)在区间[-
,
]上的图象.
(2)通过正弦函数的对称轴方程和对称中心的坐标,直接求f(x)图象的对称轴的方程和对称中心的坐标;
(3)通过列表,描点,连线在给出的直角坐标系中,请画出f(x)在区间[-
| π |
| 2 |
| π |
| 2 |
解答:解:(1)由-
+2kπ≤2x-
≤
+2kπ,
得x∈[kπ-
,kπ+
]
∴f(x)的单调增区间为[kπ-
,kπ+
].k∈Z.
(2)由2x-
=kπ+
,k∈Z,解得x=
+
,k∈Z.
∴f(x)对称轴的方程x=
+
.k∈Z.
2x-
=kπ,k∈Z.
得x=
+
.
故f(x)图象的对称中心为(
+
,1).k∈Z.…(4)
(3)由f(x)=2sin(2x-
)+1知
故f(x)在区间[-
,
]上的图象如图所示.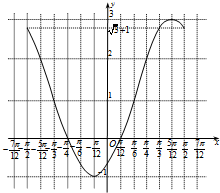
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
得x∈[kπ-
| π |
| 12 |
| 5π |
| 12 |
∴f(x)的单调增区间为[kπ-
| π |
| 12 |
| 5π |
| 12 |
(2)由2x-
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| 5π |
| 12 |
∴f(x)对称轴的方程x=
| kπ |
| 2 |
| 5π |
| 12 |
2x-
| π |
| 3 |
得x=
| kπ |
| 2 |
| π |
| 6 |
故f(x)图象的对称中心为(
| kπ |
| 2 |
| π |
| 6 |
(3)由f(x)=2sin(2x-
| π |
| 3 |
2x-
|
-
|
-π | -
|
0 |
|
| ||||||||||||
| x | -
|
-
|
-
|
|
|
| ||||||||||||
| f(x) |
|
1 | -1 | 1 | 3 |
|
| π |
| 2 |
| π |
| 2 |

点评:考查了正弦函数的单调性、对称轴以及对称中心等性质,函数图象的作法,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目