题目内容
已知f(x)=2sin(2x-
)-m在x∈[0,
]上有两个不同的零点x1,x2,则m取值范围是
.
| π |
| 6 |
| π |
| 2 |
[1,2)
[1,2)
,x1+x2=| 2π |
| 3 |
| 2π |
| 3 |
分析:令t=2x-
,由x∈[0,
],可以得到t的范围,由题意可得y=2sint 和y=m在t上,上有两个不同的交点,从而求得m的取值范围,求出函数的对称轴即可x1+x2的值;
| π |
| 6 |
| π |
| 2 |
解答: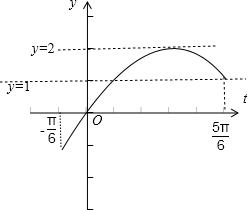 解:令t=2x-
解:令t=2x-
,由x∈[0,
],可得-
≤2x-
≤
π,解得t∈[-
,
π],
由题意可得g(t)=2sint-m 在t∈[-
,
π],上有两个不同的零点,
故 y=2sint 和y=m在t上有两个不同的交点x1,x2,如图所示:
可以得到1≤m<2,
因为x1,x2,关于x=
对称,
∴x1+x2=
,
故答案为:[1,2),
;
 解:令t=2x-
解:令t=2x-| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5 |
| 6 |
| π |
| 6 |
| 5 |
| 6 |
由题意可得g(t)=2sint-m 在t∈[-
| π |
| 6 |
| 5 |
| 6 |
故 y=2sint 和y=m在t上有两个不同的交点x1,x2,如图所示:
可以得到1≤m<2,
因为x1,x2,关于x=
| π |
| 3 |
∴x1+x2=
| 2π |
| 3 |
故答案为:[1,2),
| 2π |
| 3 |
点评:本题考查正弦函数的图象,函数的零点的判定方法,体现了数形结合及转化的数学思想,画出图形是解题的关键.

练习册系列答案
相关题目
 已知
已知