题目内容
1.函数f(x)=x3-3x2+2在区间[-1,1]上最大值为M,最小值为m,则M-m的值为( )| A. | 2 | B. | -4 | C. | 4 | D. | -2 |
分析 利用导数的正负,可得f(x)在区间[-1,1]上的单调性,求出函数的最值,作差即可.
解答 解:f′(x)=3x2-6x=3x(x-2),
令f′(x)>0,解得:x>2(舍)或x<0,
令f′(x)<0,解得:0<x<1,
故f(x)在[-1,0)递增,在(0,1]递减,
故f(x)的最大值是f(0)=2,而f(-1)=-2,f(1)=0,
故M=2,m=-2,
M-m=4,
故选:C.
点评 本题考查利用导数求函数在闭区间上的最值问题,属中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
2.如图,给出的是$1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{99}$的值的一个程序框图,判断框内应填入的条件是( )
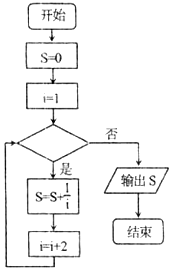

| A. | i<99 | B. | i≤99 | C. | i>99 | D. | i≥99 |
19.已知A,B是单位圆O上的两个动点,|AB|=$\sqrt{2}$,$\overrightarrow{OC}$=2$\overrightarrow{OA}$-$\overrightarrow{OB}$.若M是线段AB的中点,则$\overrightarrow{OC}$•$\overrightarrow{OM}$的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
6.已知$a=\frac{1}{2}$,$b={3^{\frac{1}{2}}}$,c=log32,则( )
| A. | b>a>c | B. | c>b>a | C. | b>c>a | D. | a>b>c |
11.某市组织一次高三调研考试,考试后统计的数学成绩服从正态分布,其密度函数为f(x)=$\frac{1}{10\sqrt{2π}}$e${\;}^{-\frac{(x-80)^{2}}{200}}$,则下列命题中不正确的是( )
| A. | 该市在这次考试的数学平均成绩为80分 | |
| B. | 分数在120分以上的人数与分数在60分以下的人数相同 | |
| C. | 分数在110分以上的人数与分数在50分以下的人数相同 | |
| D. | 该市这次考试的数学成绩标准差为10 |
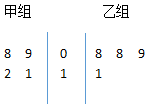 甲,乙两组各4名同学参加学校组织的“抗日战争历史知识知多少”抢答比赛,他们答对的题目个数用茎叶图表示,如图,中间一列的数字表示答对题目个数的十位数,两边的数字表示答对题目个数的个位数.
甲,乙两组各4名同学参加学校组织的“抗日战争历史知识知多少”抢答比赛,他们答对的题目个数用茎叶图表示,如图,中间一列的数字表示答对题目个数的十位数,两边的数字表示答对题目个数的个位数.