��Ŀ����
��a��b��������
������֤��
��
��
����������γ�
��
��
�ֱ�Ϊa��b����������ƽ����������ƽ����������ƽ����������ͼ��CΪ�߶�AB�ϵĵ㣬��AC=a��CB=b��OΪAB�Ĵ��߽���Բ��D������OD��AD��BD������C��OD�Ĵ��ߣ�����ΪE��ͼ���߶�OD�ij�����a��b������ƽ��������ֱ���ͼ���߶εij�������ʾa��b�����ļ���ƽ�����͵���ƽ��������˵�����ɣ�

������֤��
| ab |
| 2 | ||||
|
����������γ�
| a+b |
| 2 |
| ab |
| 2 | ||||
|

��I��֤��������a��b��Ϊ���������ݻ�������ʽ���ɵ�
��
=
����
��
��
���ҽ���a=bʱ���Ⱥų�����
��II����Rt��ADB��DCΪ�ߣ�������Ӱ�����ɵ�CD2=AC•CB��
��CD=
����CD����Ϊa��b�ļ���ƽ������
��ֱ��������OCD�У�����Ӱ�����ɵ�CD2=DE•OD��
��DE=
=
=
����DC��DE����
��
�����ҽ���a=bʱ���Ⱥų�����
���߶�DE�ij��ȷֱ�Ϊa��b�ĵ���ƽ������
| ||||
| 2 |
|
| 1 | ||
|
| ab |
| 2 | ||||
|
���ҽ���a=bʱ���Ⱥų�����
��II����Rt��ADB��DCΪ�ߣ�������Ӱ�����ɵ�CD2=AC•CB��
��CD=
| ab |
��ֱ��������OCD�У�����Ӱ�����ɵ�CD2=DE•OD��
��DE=
| DC2 |
| OD |
| ab | ||
|
| 2 | ||||
|
| ab |
| 2 | ||||
|
���߶�DE�ij��ȷֱ�Ϊa��b�ĵ���ƽ������

��ϰ��ϵ�д�
�����Ŀ
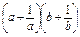 ��
��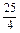 .
. ��
�� ����֤��
����֤��
 ����������
���������� �������
������� ����
���� �Ǵ���������
�Ǵ��������� ��ֵΪ�� ��
��ֵΪ�� �� ������
������ ��ģ�ǣ� ��
��ģ�ǣ� ��



 ����ô
����ô ��ʱ�����������Ӧ�ǣ� ��
��ʱ�����������Ӧ�ǣ� �� ����
���� ����
����