题目内容
数列{an}的前n项和Sn与an满足:Sn=1-nan(n∈N*),求{an}的通项公式.(注意:本题用数学归纳法做,其它方法不给分)
由题意,a1=S1=1-a1,∴a1=
=
a2=S2-S1=(1-2a2)-(1-a1),∴a2=
=
猜想an=
用数学归纳法证明如下:
(1)n=1时,结论成立;
(2)假设n=k时,结论成立,即ak=
,
则n=k+1时,ak+1=Sk+1-Sk=[1-(k+1)ak+1]-[1-k•
],
∴ak=
即猜想成立
∴an=
成立.
| 1 |
| 2 |
| 1 |
| 1×2 |
a2=S2-S1=(1-2a2)-(1-a1),∴a2=
| 1 |
| 6 |
| 1 |
| 2×3 |
猜想an=
| 1 |
| n(n+1) |
用数学归纳法证明如下:
(1)n=1时,结论成立;
(2)假设n=k时,结论成立,即ak=
| 1 |
| k(k+1) |
则n=k+1时,ak+1=Sk+1-Sk=[1-(k+1)ak+1]-[1-k•
| 1 |
| k(k+1) |
∴ak=
| 1 |
| (k+1)[(k+1)+1] |
即猜想成立
∴an=
| 1 |
| n(n+1) |

练习册系列答案
相关题目

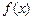 在
在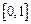 上有意义,且
上有意义,且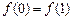 ,如果对于不同的
,如果对于不同的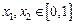 ,都有
,都有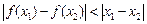 ,求证:
,求证: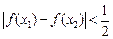 。那么他的反设应该是___________.
。那么他的反设应该是___________. 满足
满足 (
( 为虚数单位),则
为虚数单位),则 为 .
为 . 是实数(
是实数( 是虚数单位),则实数
是虚数单位),则实数 的值为( )
的值为( )



 为正整数,用数学归纳法证明
为正整数,用数学归纳法证明
 时,若已假设
时,若已假设 (
( 为偶数)真,则还需利用归纳假设再证( )
为偶数)真,则还需利用归纳假设再证( ) 时等式也成立 B
时等式也成立 B 、
、 时等式也成立
时等式也成立  时等式也成立 D、
时等式也成立 D、 时等式也成立
时等式也成立