题目内容
已知a＞0,b＞0,且a+b=1,试用分析法证明不等式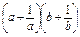
≥
.
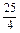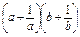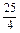≥.证明略
证明 要证≥,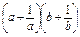
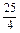只需证ab+
≥，
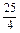只需证4(ab)2+4(a2+b2)-25ab+4≥0,
只需证4(ab)2+8ab-25ab+4≥0,
只需证4(ab)2-17ab+4≥0,
即证ab≥4或ab≤
,只需证ab≤，
而由1=a+b≥2
,∴ab≤显然成立，
所以原不等式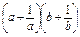≥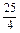成立.
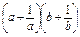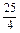≥,只需证ab+
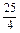≥，只需证4(ab)2+4(a2+b2)-25ab+4≥0,
只需证4(ab)2+8ab-25ab+4≥0,
只需证4(ab)2-17ab+4≥0,
即证ab≥4或ab≤
,只需证ab≤，而由1=a+b≥2
,∴ab≤显然成立，所以原不等式
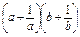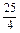≥成立.
练习册系列答案
相关题目
的倒数成等差数列，求证：角
.
；
；
；
(用含有
的式子表示，其中
，
，
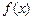在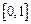
上有意义,且
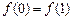,如果对于不同的
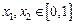,都有
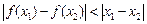，求证：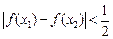
。那么他的反设应该是___________．
=
,则
是（ ） 
”时，从“
”变到 “
”时，左边应增乘的因式
是________________
_____ ；