题目内容
对于任意有理数x，y，都有|x|+|y|≥|x+y|，利用这一结论，求|x-2|+|x+4|的最小值为 ．
考点：绝对值三角不等式
专题：计算题,不等式的解法及应用
分析：根据对于任意有理数x，y，都有|x|+|y|≥|x+y|，即可得出结论．
解答：
解：∵对于任意有理数x，y，都有|x|+|y|≥|x+y|，
∴|x-2|+|x+4|=|2-x|+|x+4|≥|2-x+x+4|=6，
∴|x-2|+|x+4|的最小值为6．
故答案为：6．
∴|x-2|+|x+4|=|2-x|+|x+4|≥|2-x+x+4|=6，
∴|x-2|+|x+4|的最小值为6．
故答案为：6．
点评：本题考查绝对值三角不等式，正确运用任意有理数x，y，都有|x|+|y|≥|x+y|，是解题的关键．
练习册系列答案
相关题目
如图，边长为3的正方形ABCD中，点E，F分别为边AB，BC上的点，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于点A′．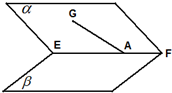
平面角为锐角的二面角α-EF-β，A∈EF，AG?α，∠GAE=45°，若AG与β所成角为30°，则二面角α-EF-β的大小是