题目内容
14.若[x]表示不超过x的最大整数,则[lg2]+[lg3]+…+lg[2017]+[lg$\frac{1}{2}$]+[lg$\frac{1}{3}$]+…+[lg$\frac{1}{2017}$]=-2013.分析 分类讨论,当2≤n≤9时,[lgn]=0;当10≤n≤99时,[lgn]=1;当100≤n≤999时,[lgn]=2;当1000≤n≤9999时,[lgn]=3;当$\frac{1}{10}$≤$\frac{1}{n}$≤$\frac{1}{2}$,[lg$\frac{1}{n}$]=-1;当$\frac{1}{100}$≤$\frac{1}{n}$≤$\frac{1}{11}$时,[lg$\frac{1}{n}$]=-2;当$\frac{1}{1000}$≤$\frac{1}{n}$≤$\frac{1}{101}$时,[lg$\frac{1}{n}$]=-3;
当$\frac{1}{10000}$≤$\frac{1}{n}$≤$\frac{1}{1001}$时,[lg$\frac{1}{n}$]=-4.从而分别求和即可.
解答 解:当2≤n≤9时,[lgn]=0,
当10≤n≤99时,[lgn]=1,
当100≤n≤999时,[lgn]=2,
当1000≤n≤9999时,[lgn]=3,
故[lg2]+[lg3]+…+[lg2016]+[2017]
=0×8+1×90+2×900+3×1018
=90+1800+3054
=4944;
当$\frac{1}{10}$≤$\frac{1}{n}$≤$\frac{1}{2}$,[lg$\frac{1}{n}$]=-1;
当$\frac{1}{100}$≤$\frac{1}{n}$≤$\frac{1}{11}$时,[lg$\frac{1}{n}$]=-2;
当$\frac{1}{1000}$≤$\frac{1}{n}$≤$\frac{1}{101}$时,[lg$\frac{1}{n}$]=-3;
当$\frac{1}{10000}$≤$\frac{1}{n}$≤$\frac{1}{1001}$时,[lg$\frac{1}{n}$]=-4.
则[lg$\frac{1}{2}$]+[lg$\frac{1}{3}$]+…+[lg$\frac{1}{2017}$]
=(-1)×9+(-2)×90+(-3)×900+(-4)×1017
=-6957,
故原式=4944-6957=-2013.
故答案为:-2013.
点评 本题以新定义为载体,主要考查了对数函数值的基本运算,解题的关键:是对对数值准确取整的计算与理解.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | $\frac{80}{21}$ | B. | $\frac{21}{80}$ | C. | $-\frac{21}{80}$ | D. | $-\frac{80}{21}$ |
| A. | 3 | B. | -6 | C. | -$\frac{3}{2}$ | D. | $\frac{2}{3}$ |
| A. | b<a<c | B. | a<b<c | C. | b<c<a | D. | c<b<a |
| A. | $\sqrt{3}$ | B. | 3 | C. | $2\sqrt{3}$ | D. | 6 |
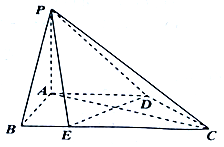 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=$\frac{1}{2}$BC=2,E在BC上,且BE=$\frac{1}{2}$AB=1,侧棱PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=$\frac{1}{2}$BC=2,E在BC上,且BE=$\frac{1}{2}$AB=1,侧棱PA⊥平面ABCD.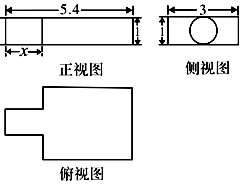 我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为1.6寸.
我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器--商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x为1.6寸.