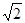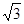题目内容
已知双曲线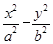 =1的离心率为2,焦点到渐近线的距离等于
=1的离心率为2,焦点到渐近线的距离等于 ,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.
,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.
(1)求双曲线的方程;
(2)若△F1AB的面积等于6 ,求直线l的方程.
,求直线l的方程.
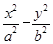 =1的离心率为2,焦点到渐近线的距离等于
=1的离心率为2,焦点到渐近线的距离等于 ,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.
,过右焦点F2的直线l交双曲线于A、B两点,F1为左焦点.(1)求双曲线的方程;
(2)若△F1AB的面积等于6
 ,求直线l的方程.
,求直线l的方程.(1)x2-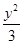 =1(2)y=±(x-2)
=1(2)y=±(x-2)
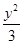 =1(2)y=±(x-2)
=1(2)y=±(x-2)学生错解:解:(2)设A(x1,y1),B(x2,y2),F(2,0),直线l:y=k(x-2),
由 消元得(k2-3)x2-4k2x+4k2+3=0,x1+x2=
消元得(k2-3)x2-4k2x+4k2+3=0,x1+x2=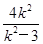 ,x1x2=
,x1x2=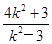 ,y1-y2=k(x1-x2),
,y1-y2=k(x1-x2),
△F1AB的面积S=c|y1-y2|=2|k|·|x1-x2|=2|k|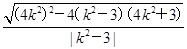 =2|k|·
=2|k|·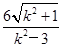 =6
=6 ,k4+8k2-9=0,k2=1,k=±1,所以直线l的方程为y=±(x-2).
,k4+8k2-9=0,k2=1,k=±1,所以直线l的方程为y=±(x-2).
审题引导:(1)直线与双曲线相交问题时的处理方法;(2)△F1AB面积的表示.
规范解答:解:(1)依题意,b= ,
,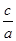 =2?a=1,c=2,(4分)
=2?a=1,c=2,(4分)
∴双曲线的方程为x2-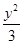 =1.(6分)
=1.(6分)
(2)设A(x1,y1),B(x2,y2),F2(2,0),直线l:y=k(x-2),
由 消元得(k2-3)x2-4k2x+4k2+3=0,(8分)
消元得(k2-3)x2-4k2x+4k2+3=0,(8分)
k≠± 时,x1+x2=
时,x1+x2=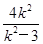 ,x1x2=
,x1x2=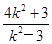 ,y1-y2=k(x1-x2),(10分)
,y1-y2=k(x1-x2),(10分)
△F1AB的面积S=c|y1-y2|=2|k|·|x1-x2|=2|k|·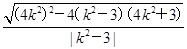 =2|k|·
=2|k|·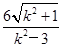 =6
=6 ,k4+8k2-9=0,k2=1,k=±1,(14分)
,k4+8k2-9=0,k2=1,k=±1,(14分)
所以直线l的方程为y=±(x-2).(16分)
错因分析:解本题时容易忽略二次项系数不为零,即k≠± 这一条件
这一条件
由
 消元得(k2-3)x2-4k2x+4k2+3=0,x1+x2=
消元得(k2-3)x2-4k2x+4k2+3=0,x1+x2=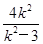 ,x1x2=
,x1x2=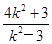 ,y1-y2=k(x1-x2),
,y1-y2=k(x1-x2),△F1AB的面积S=c|y1-y2|=2|k|·|x1-x2|=2|k|
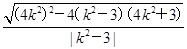 =2|k|·
=2|k|·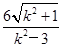 =6
=6 ,k4+8k2-9=0,k2=1,k=±1,所以直线l的方程为y=±(x-2).
,k4+8k2-9=0,k2=1,k=±1,所以直线l的方程为y=±(x-2).审题引导:(1)直线与双曲线相交问题时的处理方法;(2)△F1AB面积的表示.
规范解答:解:(1)依题意,b=
 ,
,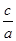 =2?a=1,c=2,(4分)
=2?a=1,c=2,(4分)∴双曲线的方程为x2-
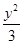 =1.(6分)
=1.(6分)(2)设A(x1,y1),B(x2,y2),F2(2,0),直线l:y=k(x-2),
由
 消元得(k2-3)x2-4k2x+4k2+3=0,(8分)
消元得(k2-3)x2-4k2x+4k2+3=0,(8分)k≠±
 时,x1+x2=
时,x1+x2=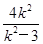 ,x1x2=
,x1x2=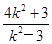 ,y1-y2=k(x1-x2),(10分)
,y1-y2=k(x1-x2),(10分)△F1AB的面积S=c|y1-y2|=2|k|·|x1-x2|=2|k|·
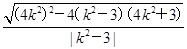 =2|k|·
=2|k|·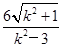 =6
=6 ,k4+8k2-9=0,k2=1,k=±1,(14分)
,k4+8k2-9=0,k2=1,k=±1,(14分)所以直线l的方程为y=±(x-2).(16分)
错因分析:解本题时容易忽略二次项系数不为零,即k≠±
 这一条件
这一条件
练习册系列答案
相关题目
 :
: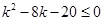 ,命题
,命题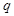 :方程
:方程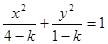 表示焦点在
表示焦点在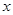 轴上的双曲线.
轴上的双曲线.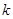 的取值范围;
的取值范围;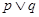 ”为真,命题“
”为真,命题“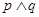 ”为假,求实数
”为假,求实数 :
: 与抛物线
与抛物线 的准线交于
的准线交于 两点,且
两点,且 ,则
,则 的值是( )
的值是( )
 .
.

 的离心率为
的离心率为 ,则实数m的值为 .
,则实数m的值为 . 的准线与双曲线
的准线与双曲线 的两条渐近线分别交于
的两条渐近线分别交于 ,
, 两点,且
两点,且 ,则双曲线的离心率
,则双曲线的离心率 为 .
为 . ,点P在双曲线上,且线段
,点P在双曲线上,且线段 的中点坐标为(
的中点坐标为( ,
, ),则此双曲线的离心率是 .
),则此双曲线的离心率是 . =1的渐近线方程为________.
=1的渐近线方程为________. x
x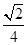 x
x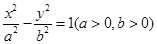 的一条渐近线与
的一条渐近线与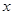 轴的夹角为
轴的夹角为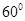 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )