题目内容
把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第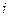 行共有
行共有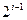 个正整数.设
个正整数.设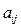 (i、j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数.
(i、j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数.
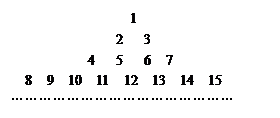
(Ⅰ)若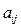 =2010,求i和j的值;
=2010,求i和j的值;
(Ⅱ)记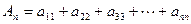
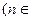 N*),试比较
N*),试比较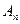 与
与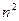
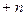 的大小,并说明理由.
的大小,并说明理由.
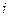 行共有
行共有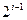 个正整数.设
个正整数.设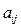 (i、j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数.
(i、j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数. 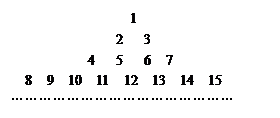
(Ⅰ)若
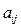 =2010,求i和j的值;
=2010,求i和j的值;(Ⅱ)记
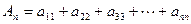
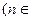 N*),试比较
N*),试比较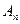 与
与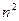
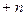 的大小,并说明理由.
的大小,并说明理由.(Ⅰ)i=11,
(Ⅱ)当 ,2,3时,
,2,3时, 当
当 时,
时,

(Ⅱ)当
 ,2,3时,
,2,3时, 当
当 时,
时,
(Ⅰ)因为数表中前i-1行共有 个数,则第i行的第一个数是
个数,则第i行的第一个数是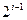 ,所以
,所以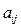 (2分)
(2分)
因为 ,
,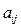 =2010,则i-1=10,即i=11. (4分)
=2010,则i-1=10,即i=11. (4分)
令 ,则
,则 . (5分)
. (5分)
(Ⅱ)因为 ,则
,则
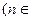 N*). (6分)
N*). (6分)
所以
 .
.
所以 . (7分)
. (7分)
检验知,当 ,2,3时,
,2,3时, ,即
,即 . (8分)
. (8分)
猜想:当 时,
时, . (9分)
. (9分)
证法一:当 时,
时, 



 . (12分)
. (12分)
综上分析,当 时,
时, ;当
;当 时,
时,
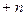 . (13分)
. (13分)
证法二:①当 时,
时, ,所以
,所以 成立. (10分)
成立. (10分)
②假设当 时,不等式成立,即
时,不等式成立,即 .
.
则 .
.
因为 ,
,
所以 ,即当
,即当 时,猜想也正确.
时,猜想也正确.
由①、②得当 时,
时,  成立.
成立.
综上分析,当 时,
时, ;当
;当 时,
时,
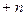 . (13分)
. (13分)
 个数,则第i行的第一个数是
个数,则第i行的第一个数是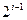 ,所以
,所以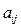 (2分)
(2分)因为
 ,
,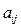 =2010,则i-1=10,即i=11. (4分)
=2010,则i-1=10,即i=11. (4分)令
 ,则
,则 . (5分)
. (5分)(Ⅱ)因为
 ,则
,则
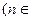 N*). (6分)
N*). (6分)所以

 .
.所以
 . (7分)
. (7分)检验知,当
 ,2,3时,
,2,3时, ,即
,即 . (8分)
. (8分)猜想:当
 时,
时, . (9分)
. (9分)证法一:当
 时,
时, 



 . (12分)
. (12分)综上分析,当
 时,
时, ;当
;当 时,
时,
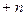 . (13分)
. (13分)证法二:①当
 时,
时, ,所以
,所以 成立. (10分)
成立. (10分)②假设当
 时,不等式成立,即
时,不等式成立,即 .
.则
 .
.因为
 ,
,所以
 ,即当
,即当 时,猜想也正确.
时,猜想也正确.由①、②得当
 时,
时,  成立.
成立. 综上分析,当
 时,
时, ;当
;当 时,
时,
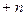 . (13分)
. (13分)
练习册系列答案
相关题目
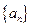 的前
的前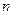 项和为
项和为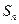 ,对任意的正整数
,对任意的正整数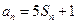 成立,记
成立,记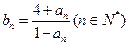 。
。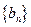 的通项公式;
的通项公式;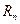 ,是否存在正整数
,是否存在正整数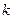 ,使得
,使得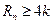 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数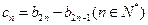 ,设数列
,设数列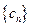 的前
的前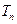 ,求证:对任意正整数
,求证:对任意正整数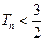 。
。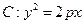 的准线方程
的准线方程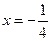 ,
,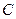 与直线
与直线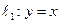 在第一象限相交于点
在第一象限相交于点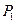 ,过
,过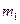 ,过
,过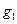 交x轴正半轴于点
交x轴正半轴于点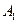 ,过
,过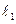 的平行线
的平行线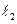 交抛物线
交抛物线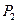 ,过
,过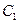 的切线
的切线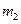 ,过
,过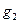 交x轴正半轴于点
交x轴正半轴于点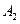 ,…,依此类推,在x轴上形成一点列
,…,依此类推,在x轴上形成一点列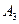 ,…,
,…,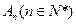 ,设点
,设点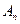 的坐标为
的坐标为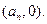
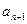 关于
关于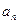 的递推关系式; (Ⅱ)求证:
的递推关系式; (Ⅱ)求证: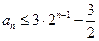 ;
;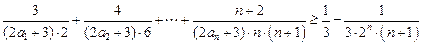 .
.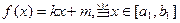 时,
时,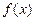 的值域为
的值域为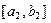 ,当
,当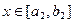
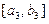 ,依次类推,一般地,当
,依次类推,一般地,当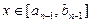 时,
时,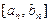 ,其中k、m为常数,且
,其中k、m为常数,且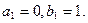
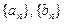 的通项公式;
的通项公式;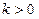 ,使得数列
,使得数列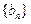 满足
满足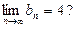 若存在,求k的值;若不存在,请说明理由;
若存在,求k的值;若不存在,请说明理由;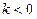 ,设数列
,设数列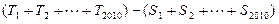 。
。 和
和 都是等差数列,其中a1=5,b1=10,且a50+b50=20,则数列
都是等差数列,其中a1=5,b1=10,且a50+b50=20,则数列 的前50项和为( )
的前50项和为( ) 为二次函数,不等式
为二次函数,不等式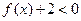 的解集为
的解集为 ,且对任意
,且对任意 ,恒有
,恒有 .
.  满足
满足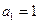 ,
,
 .
.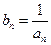 ,求数列
,求数列 的通项公式;
的通项公式; 项和为
项和为 ,求数列
,求数列 的前
的前 .
.  中,
中, ,数列
,数列 满足
满足 ,且
,且 (1)求数列
(1)求数列 的前
的前 项的和
项的和 .
. 为等差数列
为等差数列 的前
的前 项和,且
项和,且 ,
, ,则
,则 ( )
( )
