题目内容
7.已知椭圆5x2+ky2=5的一个焦点是(0,2),则椭圆的离心率等于$\frac{2\sqrt{5}}{5}$.分析 由已知得椭圆${x}^{2}+\frac{{y}^{2}}{\frac{5}{k}}=1$的一个焦点是(0,2),由此能求出$a=\sqrt{5},c=2$,从而能求出椭圆的离心率.
解答 解:∵椭圆5x2+ky2=5的一个焦点是(0,2),
∴椭圆${x}^{2}+\frac{{y}^{2}}{\frac{5}{k}}=1$的一个焦点是(0,2),
∴$\frac{5}{k}=4+1$,解得k=1,
∴$a=\sqrt{5},c=2$,
∴$e=\frac{c}{a}=\frac{2}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题考查椭圆的离心率的求法,是基础题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.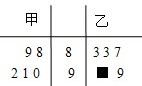 如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
 如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )
如图的茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12.已知复数z的实部为1,虚部为-2,则$\frac{5i}{z}$=( )
| A. | 2-i | B. | 2+i | C. | -2-i | D. | -2+i |
16.已知∠xOy=90°,A在Ox上,B在Oy上,且OA=OB,点P是△AOB内的动点,射线OP交线段AB于点C,则AC≥AO的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $1-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
17.在矩形ABCD中,AB=8,BC=6,沿AC将矩形ABCD折成一个45°的二面角B-AC-D,则四面体ABCD的外接球的体积为( )
| A. | $\frac{375π}{4}$ | B. | 100π | C. | $\frac{250\sqrt{2}π}{3}$ | D. | $\frac{500π}{3}$ |