题目内容
14.已知数列{an}满足an=$\left\{\begin{array}{l}{(5-a)n-11,n≤5}\\{{a}^{n-4},n>5}\end{array}\right.$,且{an}是递增数列,则实数a的取值范围是( )| A. | (1,5) | B. | ($\frac{7}{3}$,5) | C. | [$\frac{7}{3}$,5) | D. | (2,5) |
分析 {an}是递增数列,可得$\left\{\begin{array}{l}{5-a>0}\\{a>1}\\{5(5-a)-11<{a}^{2}}\end{array}\right.$,解得即可.
解答 解:{an}满足an=$\left\{\begin{array}{l}{(5-a)n-11,n≤5}\\{{a}^{n-4},n>5}\end{array}\right.$,且{an}是递增数列,
∴$\left\{\begin{array}{l}{5-a>0}\\{a>1}\\{5(5-a)-11<{a}^{2}}\end{array}\right.$,
解得2<a<5,
故选:D
点评 本题考查了函数与数列的单调性、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.在6双不同颜色的手套中任取5只,其中恰好2只为同一双的取法共有( )种.
| A. | 360 | B. | 480 | C. | 1440 | D. | 2880 |
9.已知点A(1,3),B(-5,1),直线L关于A、B对称,则L的方程是( )
| A. | 3x-y-8=0 | B. | 3x+y+4=0 | C. | 3x-y+6=0 | D. | 3x+y+2=0 |
19.已知函数f(x)=$\left\{\begin{array}{l}{kx-2,x≥0}\\{-ln(-x),x<0}\end{array}\right.$的图象上有两对关于坐标原点对称的点,则实数k的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{1}{e}$) | C. | (0,+∞) | D. | (0,e) |
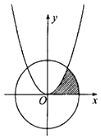 (x2+$\frac{a}{2x}$)6展开式的常数项是15,如图阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,则封闭图形面积为$\frac{π}{4}$-$\frac{1}{6}$.
(x2+$\frac{a}{2x}$)6展开式的常数项是15,如图阴影部分是由曲线y=x2和圆x2+y2=a及x轴围成的封闭图形,则封闭图形面积为$\frac{π}{4}$-$\frac{1}{6}$. 如图是一“T”型水渠的平面视图(俯视图),水渠的南北方向和东西方向轴截面均为矩形,南北向渠宽为4m,东西向渠宽$\sqrt{2}m$(从拐角处,即图中A,B处开始).假定渠内的水面始终保持水平位置(即无高度差).
如图是一“T”型水渠的平面视图(俯视图),水渠的南北方向和东西方向轴截面均为矩形,南北向渠宽为4m,东西向渠宽$\sqrt{2}m$(从拐角处,即图中A,B处开始).假定渠内的水面始终保持水平位置(即无高度差).