题目内容
已知函数f(x)=|x-a|(a>0),且不等式f(x)≥|x+1|的解集为{x|x≤
}.
(Ⅰ)求a的值;
(Ⅱ)设函数g(x)=f(x)+|2x+1|,若不等式|2m+3|+|m-3|≥|m|•g(x)对任意m∈R且m≠0恒成立,求x的取值范围.
| 1 |
| 2 |
(Ⅰ)求a的值;
(Ⅱ)设函数g(x)=f(x)+|2x+1|,若不等式|2m+3|+|m-3|≥|m|•g(x)对任意m∈R且m≠0恒成立,求x的取值范围.
考点:绝对值不等式的解法
专题:选作题,不等式
分析:(1)不等式f(x)≥|x+1|的解集为{x|x≤
},可得
是f(x)=|x+1|的解;
(2)由g(x)≤
对任意m∈R且m≠0恒成立,可得g(x)≤3,解不等式:|x-2|+|2x+1|≤3,从而解得实数x的范围.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由g(x)≤
| |2m+3|+|m-3| |
| |m| |
解答:
解:(1)不等式f(x)≥|x+1|,可化为(x-a)2≥(x+1)2,
∵不等式f(x)≥|x+1|的解集为{x|x≤
},
∴(
-a)2=(
+1)2,
∴a=2;
(2)不等式|2m+3|+|m-3|≥|m|•g(x)对任意m∈R且m≠0恒成立转化为g(x)≤
对任意m∈R且m≠0恒成立.
∵|2m+3|+|m-3|≥3|m|,
∴
≥3,
∴g(x)≤3,
∴解不等式:|x-2|+|2x+1|≤3可得x∈[-
,0].
∵不等式f(x)≥|x+1|的解集为{x|x≤
| 1 |
| 2 |
∴(
| 1 |
| 2 |
| 1 |
| 2 |
∴a=2;
(2)不等式|2m+3|+|m-3|≥|m|•g(x)对任意m∈R且m≠0恒成立转化为g(x)≤
| |2m+3|+|m-3| |
| |m| |
∵|2m+3|+|m-3|≥3|m|,
∴
| |2m+3|+|m-3| |
| |m| |
∴g(x)≤3,
∴解不等式:|x-2|+|2x+1|≤3可得x∈[-
| 2 |
| 3 |
点评:本题考查了绝对值不等式、带绝对值的函数,不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
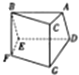 如图,已知多面体ABC-DEFG中,AB、AC、AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则下列说法中正确的个数为( )
如图,已知多面体ABC-DEFG中,AB、AC、AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1,则下列说法中正确的个数为( )