题目内容
7.不等式x2-3x+2>0的解集记为p,关于x的不等式x2+(a-1)x-a>0的解集记为q,若p是q的充分不必要条件,求实数a的取值范围.分析 根据不等式的解法求出不等式的等价条件,结合充分条件和必要条件的定义关系建立不等式关系进行求解即可.
解答 解:由不等式x2-3x+2>0得,x>2或x<1;
不等式x2+(a-1)x-a>0等价为(x-1)(x+a)>0,
①当-a≤1,即a≥-1时,不等式的解是x>1或x<-a,
∵p是q的充分不必要条件,
∴-a≥1,即a=-1,
②若-a>1,即a<-1时,不等式的解是x>-a或x<1,
∵p是q的充分不必要条件,
∴-a<2,即-2<a<-1,
综上-2<a≤-1.
点评 本题主要考查充分条件和必要条件的应用,根据不等式的性质进行求解是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.桌面上放着3个半径为1的球,两两相切,在它们上方的空间里放入一个球使其顶点(最高处)恰好和3个球的顶点在同一个平面上,该球的半径为( )
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{3}-1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
12.在长方体ABCD-A1B1C1D1中,二面角D-AB-D1的大小为45°,DC1与平面ABCD所成角的大小为30°,那么异面直线AD1与DC1所成角的余弦值是( )
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{2}}}{8}$ | D. | $\frac{{\sqrt{3}}}{8}$ |
17.把5张分别写有数字1,2,3,4,5的卡片混合,再将其任意排成一行,则得到的数能被2或5整除的概率是( )
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
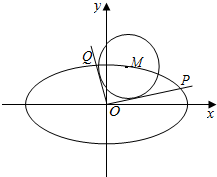 如图,已知M(x0,y0)是椭圆C:$\frac{x^2}{6}+\frac{y^2}{3}=1$上的任一点,从原点O向圆M:${({x-{x_0}})^2}+{({y-{y_0}})^2}=2$作两条切线,分别交椭圆于点P、Q.
如图,已知M(x0,y0)是椭圆C:$\frac{x^2}{6}+\frac{y^2}{3}=1$上的任一点,从原点O向圆M:${({x-{x_0}})^2}+{({y-{y_0}})^2}=2$作两条切线,分别交椭圆于点P、Q.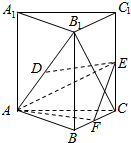 已知三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AB=AC,D,E,F分别为B1A,C1C,BC的中点.
已知三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AB=AC,D,E,F分别为B1A,C1C,BC的中点.