题目内容

15．已知点F（2，0）是椭圆3kx2+y2=1的一个焦点，则实数k的值是$\frac{1}{15}$．

分析 由题设条件知a2=$\frac{1}{3k}$，b2=1，求出c，列出方程求出k．

解答 解：椭圆3kx2+y2=1，
即为$\frac{{x}^{2}}{\frac{1}{3k}}$+y2=1，
由题意可得c=2，
则$\frac{1}{3k}$-1=4，
解得k=$\frac{1}{15}$，
故答案为：$\frac{1}{15}$．

点评 本题考查椭圆的方程和性质及应用，考查运算能力，属于基础题．

练习册系列答案
相关题目
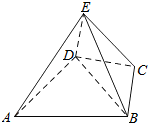1．如图，几何体E-ABCD是四棱锥，△ABD为正三角形，CB=CD，EC⊥BD．
（1）求证：BE=DE；
（2）若∠BCD=120°，是否在线段AE上存在一点M，使得DM∥平面EBC，若存在，请指出点M的位置；若不存在，请说明理由．
6．已知函数f（x）=ln（x+1）-f（0）x-f′（0）x2+2
（1）求f（x）的解析式及减区间；
（2）若f（x）≤x2+ax+b，求$\frac{b-3}{a+2}$的最小值．
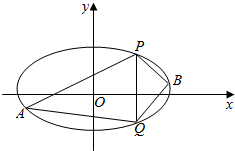3．已知椭圆C的中心在坐标原点，离心率为$\frac{1}{2}$，且它的短轴端点恰好是双曲线$\frac{y^2}{8}-\frac{x^2}{4}=1$的焦点．
（I）求椭圆C的标准方程；
（Ⅱ）如图，已知直线x=2与椭圆C相交于两点P，Q，点A，B是椭圆C上位于直线PQ两侧的动点，且总满足∠APQ=∠BPQ，试问直线AB的斜率是否为定值？若是，请求出此定值．若不是，请说明理由．
10．由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆C1：$\frac{x^2}{4}+{y^2}$=1．
（1）若椭圆C2：$\frac{x^2}{16}+{\frac{y}{4}^2}$=1，判断C2与C1是否相似？如果相似，求出C2与C1的相似比；如果不相似，请说明理由；
（2）写出与椭圆C1相似且短半轴长为b的椭圆Cb的方程；若在椭圆Cb上存在两点M、N关于直线y=x+1对称，求实数b的取值范围．
20．过抛物线$y=\frac{1}{4}{x^2}$的焦点的直线与抛物线交于A，B两点，O是抛物线的顶点．
（1）判断抛物线的准线和以AB为直径的圆的位置关系；
（2）求$\overrightarrow{OA}•\overrightarrow{OB}$的值．
7．不等式x2-3x+2＞0的解集记为p，关于x的不等式x2+（a-1）x-a＞0的解集记为q，若p是q的充分不必要条件，求实数a的取值范围．
4．已知函数f（x）=loga$\frac{λx-2}{x+2}$为奇函数（其中a＞0且a≠1，λ为常数）．
（1）求出λ的值；
（2）设g（x）=log${\;}_{\frac{1}{2}}$（$\frac{λx-2}{x+2}$•$\frac{1}{x-4}$）（x＞5），求g（x）的值域；
（3）设φ（x）=loga$\frac{λx-2}{x+2}$是定义域[m，n]上的单调递增减函数，其值域为[logaa（n-1），logaa（m-1）]，求a的取值范围．
5．若点P是曲线y2=4x上的一个动点，则点P到点A（0，1）的距离与点P到y轴的距离之和的最小值为（　　）
A．$\sqrt{2}$B．$\sqrt{2}-1$C．$\sqrt{2}+1$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网