题目内容
7.在装有相等数量的白球和黑球的口袋中放进一个白球,此时由这个口袋中取出一个白球的概率比原来由此口袋中取出一个白球的概率大$\frac{1}{22}$,则口袋中原有小球的个数为( )| A. | 5 | B. | 6 | C. | 10 | D. | 11 |
分析 设口袋中原有小球的个数为2x个,即装有白球x个和黑球x个口袋中放进一个白球,由此时由这个口袋中取出一个白球的概率比原来由此口袋中取出一个白球的概率大$\frac{1}{22}$,列出方程能求出口袋中原有小球的个数.
解答 解:设口袋中原有小球的个数为2x个,
即装有白球x个和黑球x个口袋中放进一个白球,
此时由这个口袋中取出一个白球的概率比原来由此口袋中取出一个白球的概率大$\frac{1}{22}$,
∴$\frac{x+1}{2x+1}-\frac{x}{2x}=\frac{1}{22}$,
解得x=5,
∴口袋中原有小球的个数为2x=10.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
15.已知向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$•$\overrightarrow{b}$的值为( )
| A. | -4 | B. | 8 | C. | -1 | D. | -7 |
2.若直线l1:(m-2)x-y-1=0,与直线l2:3x-my=0互相平行,则m的值等于( )
| A. | 0或-1或3 | B. | 0或3 | C. | 0或-1 | D. | -1或3 |
19.执行如图所示的程序框图,当输入x为16时,输出的y=( )
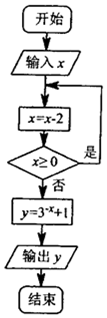

| A. | 28 | B. | 10 | C. | 4 | D. | 2 |