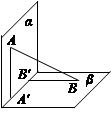题目内容
已知两个不重合的平面 ,给定以下条件:
,给定以下条件:
① 内不共线的三点到
内不共线的三点到 的距离相等;②
的距离相等;② 是
是 内的两条直线,且
内的两条直线,且 ;
;
③ 是两条异面直线,且
是两条异面直线,且 ;
;
其中可以判定 的是( )
的是( )
| A.① | B.② | C.①③ | D.③ |
D
解析试题分析:对于① 内不共线的三点到
内不共线的三点到 的距离相等,那么两个平面可以相交,故错误。
的距离相等,那么两个平面可以相交,故错误。
对于② 是
是 内的两条直线,且
内的两条直线,且 ;只有当l,m是相交直线的时候可以推出平行,故不成立。
;只有当l,m是相交直线的时候可以推出平行,故不成立。
对于③ 是两条异面直线,且
是两条异面直线,且 ,满足线面平行的判定定理,故成立,选D.
,满足线面平行的判定定理,故成立,选D.
考点:空间中点线面的位置关系
点评:解决该试题的关键是熟练的掌握线面和面面的平行、垂直的判定定理和性质定理来得到。

练习册系列答案
相关题目
设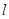 ,
,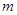 是两条不同的直线,
是两条不同的直线,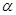 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若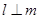 , ,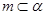 ,则 ,则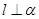 | B.若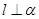 , ,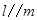 ,则 ,则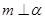 |
C.若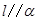 , ,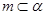 ,则 ,则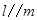 | D.若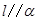 , ,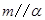 ,则 ,则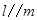 |
正方体 中
中 与截面
与截面 所成的角是
所成的角是
A. | B. | C. | D. |
已知m、n是两条不同的直线,α、β、γ是三个不同的平面,则下列命题正确的是 ( )
| A.若α⊥γ,α⊥β,则γ∥β | B.若m∥n,m?α,n?β,则α∥β |
| C.若m∥n,m∥α,则n∥α | D.若m∥n,m⊥α,n⊥β,则α∥β |
椭圆 的长轴为
的长轴为
 ,短轴为
,短轴为
 ,将椭圆沿y轴折成一个二面角,使得
,将椭圆沿y轴折成一个二面角,使得 点在平面
点在平面

 上的射影恰好为椭圆的右焦点,则该二面角的大小为( ).
上的射影恰好为椭圆的右焦点,则该二面角的大小为( ).
| A.75° | B.60° | C.45° | D.30° |
如图长方体中,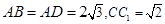 ,则二面角
,则二面角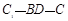 的大小为
的大小为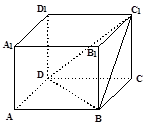
| A.300 | B.450 | C.600 | D.900 |
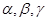 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: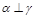 ,
,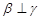 ,则
,则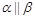 ;
;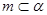 ,
,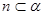 ,
,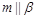 ,
,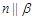 ,则
,则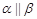 ;
;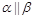 ,
,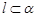 ,则
,则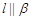 ;
;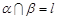 ,
,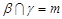 ,
,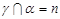 ,
,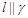 ,则
,则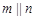 其中真命
其中真命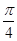 和
和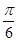 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )
,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )