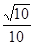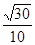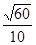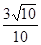题目内容
设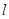 ,
,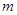 是两条不同的直线,
是两条不同的直线,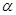 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若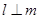 , ,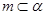 ,则 ,则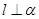 | B.若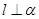 , ,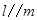 ,则 ,则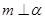 |
C.若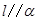 , ,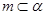 ,则 ,则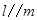 | D.若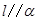 , ,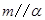 ,则 ,则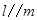 |
B
解析试题分析:根据题意,依次分析选项:A,根据线面垂直的判定定理判断.C:根据线面平行的判定定理判断.D:由线线的位置关系判断.B:由线面垂直的性质定理判断;综合可得答案
A,根据线面垂直的判定定理,要垂直平面内两条相交直线才行,不正确;
C:l∥α,m?α,则l∥m或两线异面,故不正确.
D:平行于同一平面的两直线可能平行,异面,相交,不正确.
B:由线面垂直的性质可知:平行线中的一条垂直于这个平面则另一条也垂直这个平面.故正确.
故选B
考点:立体几何中线面之间的位置关系
点评:本题主要考查了立体几何中线面之间的位置关系及其中的公理和判定定理,也蕴含了对定理公理综合运用能力的考查,属中档题

练习册系列答案
相关题目
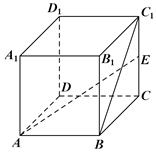
长方体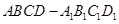 中,
中,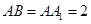 ,
,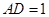 ,
,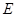 为
为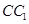 的中点,则异面直线
的中点,则异面直线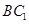 与
与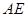 所成角的余弦值为
所成角的余弦值为
A.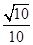 | B.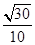 | C.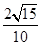 | D.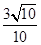 |
下面四个命题:
①若直线 平面
平面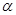 ,则
,则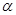 内任何直线都与
内任何直线都与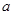 平行;
平行;
②若直线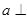 平面
平面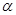 ,则
,则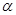 内任何直线都与
内任何直线都与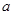 垂直;
垂直;
③若平面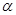
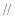 平面
平面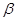 ,则
,则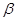 内任何直线都与
内任何直线都与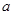 平行;
平行;
④若平面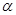
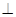 平面
平面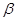 ,则
,则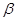 内任何直线都与
内任何直线都与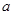 垂直。
垂直。
其中正确的两个命题是( )
| A.①② | B.②③ | C.③④ | D.②④ |
设 ,
, 是两条不同的直线,
是两条不同的直线, ,
, ,
, 是三个不同的平面.有下列四个命题:
是三个不同的平面.有下列四个命题:
①若 ,
, ,
, ,则
,则 ;②若
;②若 ,
, ,则
,则 ;
;
③ 若 ,
, ,
, ,则
,则 ;④ 若
;④ 若 ,
, ,
, ,则
,则 .
.
其中错误命题的序号是( )
| A.①④ | B.①③ | C.②③④ | D.②③ |
如图所示,正方体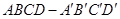 的棱长为1,O是平面
的棱长为1,O是平面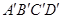 的中心,则O到平面
的中心,则O到平面 的距离是( )
的距离是( )
A.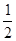 | B.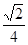 | C.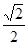 | D.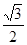 |
 、
、 是不同的直线,
是不同的直线, 、
、 、
、 是不同的平面,有以下四命题:
是不同的平面,有以下四命题:
① 若 ,则
,则 ; ②若
; ②若 ,则
,则 ;
;
③ 若 ,则
,则 ; ④若
; ④若 ,则
,则 .
.
其中真命题的序号是 ( )
| A.①③ | B.①④ | C.②③ | D.②④ |
三棱锥 中,
中, ,
, 是等腰直角三角形,
是等腰直角三角形, .若
.若 为
为 中点,则
中点,则 与平面
与平面 所成的角的大小等于( )
所成的角的大小等于( )
A. | B. | C. | D. |
 ,给定以下条件:
,给定以下条件: 内不共线的三点到
内不共线的三点到 的距离相等;②
的距离相等;② 是
是 ;
; ;
; 的是( )
的是( )