题目内容
四棱锥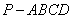 中,
中,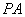 ⊥底面
⊥底面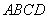 ,
,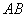 //
//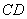 ,
,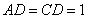 ,
,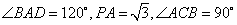
(1)求证: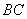 ⊥平面
⊥平面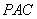 ;
;
(2)求二面角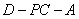 D的平面角的余弦值;
D的平面角的余弦值;
(3)求点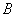 到平面
到平面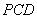 的距离。
的距离。
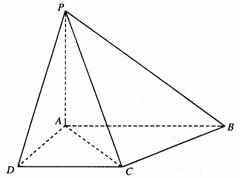
 证明:(I)∵PA⊥底面ABCD,
证明:(I)∵PA⊥底面ABCD, 平面ABCD,
平面ABCD,
∴PA⊥BC
∵∠ACB=90°
∴BC⊥AC
又
∴BC⊥平面PAC
解:(II)取CD的中点E,则AE⊥CD
∴AE⊥AB
又PA⊥底面ABCD, 底面ABCD
底面ABCD
∴PA⊥AE
建立空间直角坐标系,如图。则

A(0,0,0),


设 为平面PAC的一个法向量
为平面PAC的一个法向量
 为平面PDC的一个法向量,则
为平面PDC的一个法向量,则
 ,
,
可取 ;
;
 ,可取
,可取


(III)又B(0,2,0),
由(II)取平面PCD的一个法向量
∴点B到平面PCD的距离为



练习册系列答案
相关题目
 是偶函数,当
是偶函数,当 时,函数
时,函数 单调递减,设
单调递减,设 ,则a,b,c的大小关系为( )
,则a,b,c的大小关系为( ) ,且
,且 ,则实数
,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 到直线
到直线 的距离不大于
的距离不大于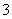 ,则
,则 的取值范围是
的取值范围是  B.
B.
 D.
D.
 上有一点
上有一点 ,它到点
,它到点 和点
和点 的距离之和最小,则点
的距离之和最小,则点 =0,则△ABC是( ).
=0,则△ABC是( ). ,|b|=3,a与b的夹角为45°,当向量a+λb与λa+b的夹角为锐角时,求实数A的范围.
,|b|=3,a与b的夹角为45°,当向量a+λb与λa+b的夹角为锐角时,求实数A的范围. ,则下列不等式①a+b>ab;②|a|>|b|;③a<b④
,则下列不等式①a+b>ab;②|a|>|b|;③a<b④ 中,正确的不等式有 ( )
中,正确的不等式有 ( )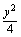 =1,过点M(0,1)的直线l交椭圆于点A、B、O是坐标原点,点P满足
=1,过点M(0,1)的直线l交椭圆于点A、B、O是坐标原点,点P满足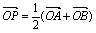 ,点N的坐标为(
,点N的坐标为(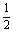 ,
, (Ⅰ)动点户的轨迹方程;
(Ⅰ)动点户的轨迹方程;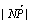 的最小值与最大值.
的最小值与最大值.