题目内容
已知椭圆C:
+
=1上有一点P(1,
),点M,N是椭圆C上的两个动点,当直线PM的斜率与直线PN的斜率互为相反数时,直线MN的斜率为 .
| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| 2 |
考点:直线的斜率
专题:计算题,综合题,圆锥曲线的定义、性质与方程
分析:设直线AM方程代入椭圆方程,利用点A(1,
)在椭圆上,可求M的坐标,利用直线AN的斜率与AM的斜率互为相反数,可求N的坐标,从而可得直线MN的斜率,问题得解.
| 3 |
| 2 |
解答:
解:设直线AM方程:得y=k(x-1)+
,
代入椭圆方程,消元可得(3+4k2)x2+4k(3-2k)x+4(
-k)2-12=0
设M(x1,y1),N(x2,y2).
因为点A(1,
)在椭圆上,
所以x1=
,y1=kx1+
-k.
又直线AN的斜率与AM的斜率互为相反数,在上式中以-k代k,
可得x2=
,y2=-kx2+
+k.
所以直线MN的斜率kMN=
=
.
即直线MN的斜率为定值,其值为
.
故答案为:
.
| 3 |
| 2 |
代入椭圆方程,消元可得(3+4k2)x2+4k(3-2k)x+4(
| 3 |
| 2 |
设M(x1,y1),N(x2,y2).
因为点A(1,
| 3 |
| 2 |
所以x1=
4(
| ||
| 3+4k2 |
| 3 |
| 2 |
又直线AN的斜率与AM的斜率互为相反数,在上式中以-k代k,
可得x2=
4(
| ||
| 3+4k2 |
| 3 |
| 2 |
所以直线MN的斜率kMN=
| y2-y1 |
| x2-x1 |
| 1 |
| 2 |
即直线MN的斜率为定值,其值为
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查直线斜率的求解,解题的关键是直线与椭圆方程联立,确定点的坐标,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
+(x-1)0的定义域为( )
| ||
| x-2 |
| A、{x|x≥1} |
| B、{x|x≥1 且x≠2} |
| C、{x|x>1} |
| D、{x|x>1 且x≠2} |
若直线x-2y+5=0与直线2x+my-6=0互相垂直,则实数m等于( )
| A、1 | ||
| B、2 | ||
| C、4 | ||
D、
|
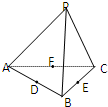 空间四边形PABC的各边及对角线长度都相等,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )
空间四边形PABC的各边及对角线长度都相等,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )| A、DF∥平面PBC |
| B、AB⊥平面PDC |
| C、平面PEF⊥平面ABC |
| D、平面PAE平面PBC |