题目内容
14.已知命题p:“不等式x2-mx+m+3>0的解集为R”;命题q:“$\frac{x^2}{m-9}+\frac{y^2}{m+1}=1$表示焦点在y轴上的双曲线”,若“p∨q”为真,“p∧q”为假,求实数m的取值范围.分析 分别化简命题p与q,由于“p∨q”为真,“p∧q”为假,可得p,q一真一假.
解答 解:命题p为真时,等价于判别式△=m2-4(m+3)<0,即-2<m<6.
命题q为真时,等价于$\left\{\begin{array}{l}m+1>0\\ m-9<0\end{array}\right.$,即-1<m<9.
依题意,p,q一真一假.
当p真,q假时,$\left\{\begin{array}{l}-2<m<6\\ m≤-1,或m≥9.\end{array}\right.$即-2<m≤-1.
当p假,q真时,$\left\{\begin{array}{l}m≤-2,或m≥6\\-1<m<9.\end{array}\right.$即6≤m<9.
综上,m的取值范围是(-2,-1]∪[6,9).
点评 本题考查了椭圆与双曲线的标准方程及其性质、复合命题真假的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.某企业生产A、B两种产品,现有资源如下:煤360吨,水300吨,电200千瓦.每生产1吨A产品需消耗煤9吨,水3吨,电4千瓦,利润7万元;每生产1吨B产品需消耗煤4吨,水10吨,电5千瓦,利润12万元.
(Ⅰ)根据题目信息填写下表:
(Ⅱ)设分别生产A、B两种产品x吨、y吨,总产值为z万元,请列出x、y满足的不等式组及目标函数.
(Ⅲ)试问该企业利用现有资源,生产A、B两种产品各多少吨,才能获得最大利润?
(Ⅰ)根据题目信息填写下表:
| 每吨产品 | 煤(吨) | 水(吨) | 电(千瓦) |
| A | |||
| B |
(Ⅲ)试问该企业利用现有资源,生产A、B两种产品各多少吨,才能获得最大利润?
2.在△ABC中,角A,B,C所对的边分别为a,b,c,若$\frac{a}{b}=2cosC$,则△ABC的形状为( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
9.设是圆P:(x+$\sqrt{5}$)2+y2=36上一动点,点Q的坐标为($\sqrt{5}$,0),若线段MQ的垂直平分线交直线PM于点N,则点N的轨迹为( )
| A. | 圆 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
19.已知sinα=$\frac{5}{13}$,α为第二象限角,tanα=( )
| A. | -$\frac{5}{12}$ | B. | $\frac{5}{12}$ | C. | -$\frac{12}{5}$ | D. | $\frac{12}{5}$ |
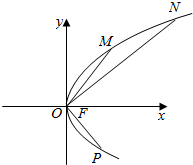 已知F是抛物线C:y2=2px(p>0)的焦点,O为坐标原点.
已知F是抛物线C:y2=2px(p>0)的焦点,O为坐标原点.