题目内容
计算：（lg5）2+lg2×lg5+lg2．
考点：对数的运算性质
专题：函数的性质及应用
分析：利用lg2+lg5=1即可得出．
解答：
解：原式=lg5（lg5+lg2）+lg2
=lg5+lg2
=1．
=lg5+lg2
=1．
点评：本题考查了lg2+lg5=1性质，属于基础题．
练习册系列答案
相关题目
若0＜α＜
，-
＜β＜0，cos（
+α）=
，cos（
-β）
，则cos（α+β）=（ ）
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 3 |
| π |
| 4 |
| ||
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
设集合M={x||x-3|＜2}，N={x|y=
}，则M∩N=（ ）
| x-2 |
| A、[2，5） |
| B、（1，5） |
| C、（2，5] |
| D、[1，5） |
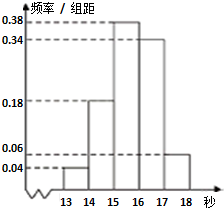南山中学高二某班50名学生在一次百米测试中，成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．