题目内容
7.Sn为数列{an}的前n项和,已知Sn+1=λSn+1(λ是大于0的常数),且a1=1,a3=4.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=nan,求数列{bn}的前n项和.
分析 (Ⅰ)由已知数列递推式可得当n≥2时,Sn=λSn-1+1.与原递推式作差可得an+1=λan,即n≥2时$\frac{{{a_{n+1}}}}{a_n}=λ$.验证a2=λa1,可得数列{an}是等比数列.结合已知求得λ值,则数列{an}的通项公式可求;
(Ⅱ)把(Ⅰ)中求得的通项公式代入bn=nan,整理后利用错位相减法求数列{bn}的前n项和.
解答 解:(Ⅰ)由Sn+1=λSn+1可知 当n≥2时,Sn=λSn-1+1.
作差可得an+1=λan,即n≥2时$\frac{{{a_{n+1}}}}{a_n}=λ$.
又a1=1,故a2=λa1.
∴数列{an}是等比数列.
由于a3=a1λ2=4,λ>0,解得λ=2.
数{an}的通项公式为:${a_n}={2^{n-1}}$;
(Ⅱ)由${a_n}={2^{n-1}}$,可知${b_n}=n•{2^{n-1}}$.
设数列{bn}前n项和为Tn,
则${T_n}=1•{2^0}+2•{2^1}+3•{2^2}+…+(n-1)•{2^{n-2}}+n•{2^{n-1}}$,①
$2{T_n}=1•2+2•{2^2}+…+(n-2)•{2^{n-2}}+(n-1)•{2^{n-1}}+n•{2^n}$,②
①-②得:$-{T_n}=1+2+{2^2}+…+{2^{n-2}}+{2^{n-1}}-n•{2^n}$=$\frac{1×(1-{2}^{n})}{1-2}-n•{2}^{n}$=2n-1-n•2n.
∴${T_n}=n•{2^n}-{2^n}+1$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了错位相减法求数列的前n项和,是中档题.

练习册系列答案
相关题目
17.某淘宝商城专营店经销某种产品,已知每个月的利润Y(单位:万元)是关于该月的交易量X(单位:件)的一次函数,当X=150时,Y=4,且X每增加100,Y增加2.该店记录了连续12个月的交易量X,整理得如表:
(1)求a的值;
(2)求这12个月的月利润(单位:万元)的平均数;
(3)假定以这12个月记录的各交易量的频率作为各交易量发生的概率,求2017年3月份该产品利润不低于5万元的概率.
| 交易量X(件) | 150 | 180 | 200 | 250 | 320 |
频率 | $\frac{1}{12}$ | $\frac{1}{6}$ | a | $\frac{1}{4}$ | $\frac{1}{6}$ |
(2)求这12个月的月利润(单位:万元)的平均数;
(3)假定以这12个月记录的各交易量的频率作为各交易量发生的概率,求2017年3月份该产品利润不低于5万元的概率.
2.平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{2π}{3}$,$\overrightarrow a=(2,0)$,$|\overrightarrow b|=1$,则$|\overrightarrow a+2\overrightarrow b|$=( )
| A. | 1 | B. | 2 | C. | $2\sqrt{3}$ | D. | 4 |
16.在区间[0,1]上任选两个数x和y,则$y≥\sqrt{1-{x^2}}$的概率为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{4}$ |
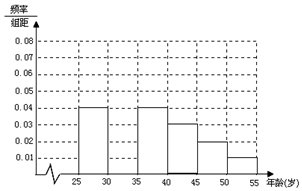 智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:
智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图: