题目内容
17. 如图,三棱锥PABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$,AC=2.D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2EB=2.
如图,三棱锥PABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$,AC=2.D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2EB=2.证明:(1)求三棱锥PABC的体积;
(2)证明DE⊥平面PCD.
分析 (1)作DF⊥BC,垂足为F,根据平行线的性质得出比例式计算AC,再代入体积公式计算三棱锥P-ABC的体积;
(2)根据勾股定理得出DE⊥CD,又PC⊥平面ABC得出PC⊥DE,故DE⊥平面PCD.
解答 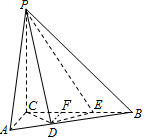 解:(1)∵CD=DE=$\sqrt{2}$,CE=2EB=2,
解:(1)∵CD=DE=$\sqrt{2}$,CE=2EB=2,
∴CE2=CD2+DE2,
∴∠CDE=90°.
作DF⊥BC,垂足为F,则DF=$\frac{1}{2}$CE=1,
∵∠ACB=$\frac{π}{2}$,
∴DF∥AC,
∴$\frac{DF}{AC}$=$\frac{2}{3}$,
∴AC=$\frac{3}{2}$.
∴VP-ABC=$\frac{1}{3}$S△ABC•PC=$\frac{1}{3}$×$\frac{1}{2}$×3×$\frac{3}{2}$×3=$\frac{9}{4}$;
(2)证明:由PC⊥平面ABC,DE?平面ABC,
得PC⊥DE
由CE=2,CD=DE=$\sqrt{2}$,得△CDE为等腰直角三角形,
故CD⊥DE.
由PC∩CD=C,DE垂直于平面PCD内两条相交直线,
故DE⊥平面PCD.
点评 本题考查了线面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
2.若[x]表示不超过x的最大整数,则图中的程序框图运行之后输出的结果为( )


| A. | 49850 | B. | 49900 | C. | 49800 | D. | 49950 |
 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径 某学校对学生的考试成绩作抽样调查,得到成绩的频率分布直方图如图所示,记[90,100]为A组,[80,90)为B组,[70,80)为C组,其中A组与[40,50)对应的数值相同,B组与[60,70)对应的数值相同,[70,80)对应的数值被污损,记为x.
某学校对学生的考试成绩作抽样调查,得到成绩的频率分布直方图如图所示,记[90,100]为A组,[80,90)为B组,[70,80)为C组,其中A组与[40,50)对应的数值相同,B组与[60,70)对应的数值相同,[70,80)对应的数值被污损,记为x. 右边程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值,执行如图所示的程序框图,若输入a0=1,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出y的值为( )
右边程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值,执行如图所示的程序框图,若输入a0=1,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出y的值为( )