题目内容
8. 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径(1)求证:AC•BC=AD•AE;
(2)过点C作⊙O的切线交BA的延长线于点F,若BC=5,CF=6,求AC的长.
分析 (1)如图所示,连接BE.由于AE是⊙O的直径,可得∠ABE=90°.利用∠E与∠ACB都是$\widehat{AB}$所对的圆周角,可得∠E=∠ACB.进而得到△ABE∽△ADC,即可得到.
(II)利用切割线定理可得CF2=AF•BF,可得BF.再利用△AFC∽△CFB,可得$\frac{AF}{FC}$=$\frac{AC}{BC}$,即可得出.
解答 (1)证明:如图所示,连接BE.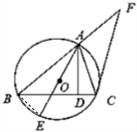
∵AE是⊙O的直径,∴∠ABE=90°.
又∠E与∠ACB都是$\widehat{AB}$所对的圆周角,∴∠E=∠ACB.
∵AD⊥BC,∠ADC=90°.
∴△ABE∽△ADC,∴$\frac{AB}{AD}$=$\frac{AE}{AC}$,∴AB•AC=AD•AE.
又AB=BC,∴BC•AC=AD•AE.
(2)∵CF是⊙O的切线,∴CF2=AF•BF,
∵AF=2,CF=4,∴42=2BF,解得BF=8.
∴AB=BF-AF=6.∵∠ACF=∠FBC,∠CFB=∠AFC,∴△AFC∽△CFB,
∴$\frac{AF}{FC}$=$\frac{AC}{BC}$,∴$AC=\frac{AF•BC}{CF}$=3.
点评 本题考查了圆的性质、三角形相似判定与性质、切割线定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
18.已知圆C的圆心位于直线x+y=0上,且圆C与直线x-y=0和直线x-y-4=0均相切,则圆的方程为( )
| A. | (x+1)2+(y-1)2=2 | B. | (x-1)2+(y+1)2=2 | C. | (x+1)2+(y+1)2=2 | D. | (x-1)2+(y-1)2=2 |
3.已知函数f(x)=ex-ax有两个零点x1<x2,则下列说法正确的个数是( )
①a>e;②x1+x2>2;③x1x2>1;④函数f(x)有极小值点x0,x1+x2<2x0.
①a>e;②x1+x2>2;③x1x2>1;④函数f(x)有极小值点x0,x1+x2<2x0.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.如果两条直线a和b没有公共点,那么a和b( )
| A. | 共面 | B. | 平行 | C. | 异面 | D. | 平行或异面 |
 已知函数f(x)=Asin(wx+φ)+B(A>0,w>),|φ|<$\frac{π}{2}$) 的部分图象如图所示:
已知函数f(x)=Asin(wx+φ)+B(A>0,w>),|φ|<$\frac{π}{2}$) 的部分图象如图所示: 如图,三棱锥PABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$,AC=2.D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2EB=2.
如图,三棱锥PABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$,AC=2.D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2EB=2.