题目内容
5.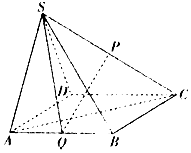 如图,在四棱锥S-ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD.(1)求证:PQ∥平面SAD;
(2)求证:SQ⊥AC.
分析 (1)取SD中点F,连结AF,PF.证明PQ∥AF.利用直线与平面平行的判定定理证明PQ∥平面SAD.
(2)连结BD,证明SE⊥AD.推出SE⊥平面ABCD,得到SE⊥AC.证明EQ⊥AC,然后证明AC⊥平面SEQ,即可证明结论.
解答 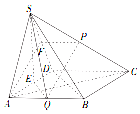 证明:(1)取SD中点F,连结AF,PF.
证明:(1)取SD中点F,连结AF,PF.
∵P,F分别是棱SC,SD的中点,∴FP∥CD,且$FP=\frac{1}{2}CD$,
∵在正方形ABCD中,Q是AB的中点,
∴AQ∥CD,且$AQ=\frac{1}{2}CD$,即FP∥AQ且FP=AQ,
∴AQPF为平行四边形,则PQ∥AF,
∵PQ?平面SAD,AF?平面SAD,∴PQ∥平面SAD.…(6分)
(2)连结BD,∵ABCD是正方形,∴AC⊥BD,
取AD中点E,连SE,EQ,
∵Q为AB中点,∴EQ∥BD,∴AC⊥EQ.
∵SA=SD,∴SE⊥AD,
∵平面SAD⊥平面ABCD,且交线为AD,∴SE⊥平面ABCD,
又AC?平面ABCD,∴AC⊥SE,
∵SE∩EQ=E,SE,EQ?平面SEQ,∴AC⊥平面SEQ,
∵SQ?平面SEQ,∴SQ⊥AC.…(12分)
点评 本题考查直线与平面平行以及直线与平面垂直的判定定理的应用,棱锥的体积的求法,考查计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列两组变量具有相关关系的是( )
| A. | 人的体重与学历 | B. | 圆的半径与其周长 | ||
| C. | 人的生活水平与购买能力 | D. | 成年人的财富与体重 |
16.心理学家分析发现“喜欢空间现象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按层抽样的方法抽取50名同学(男生30人,女生20人),给每位同学立体几何体,代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如表:(单位:人)
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为$\frac{4}{5}$,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
附表及公式:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 立体几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
(2)经统计得,选择做立体几何题的学生正答率为$\frac{4}{5}$,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
附表及公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13.设集合A={1,2,3},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件Cn(2≤n≤6,n∈N),若事件Cn的概率最大,则n的所有可能值为( )
| A. | 4 | B. | 2和6 | C. | 3和5 | D. | 3 |
20.设函数f(x)=-2x,g(x)=lg(ax2-2x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | (-1,0) | B. | (0,1) | C. | (-∞,1] | D. | [1,+∞) |
10.当下面的程序段输出结果是41,则横线处应填( )


| A. | i>4 | B. | i>=4 | C. | i<4 | D. | i<=4 |
17.若$tan({α+\frac{π}{4}})=2$,则$\frac{sinα-cosα}{sinα+cosα}$=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | $-\frac{1}{2}$ |
14.已知点M(5,-6)和向量$\overrightarrow{a}$=(1,-2),若$\overrightarrow{NM}$=3$\overrightarrow{a}$,则点N的坐标为( )
| A. | (2,0) | B. | (-3,6) | C. | (6,2) | D. | (-2,0) |