题目内容
10．某几何体的三视图如图所示，则该几何体的体积是（ ）
| A． | 16π-16 | B． | 8π-8 | C． | 16π-8 | D． | 8π-16 |
分析 由已知中的三视图可得该几何体为一个圆柱挖去一个四棱柱所得的组合体，代入柱体体积公式，可得答案．
解答 解：由已知中的三视图可得该几何体为一个圆柱挖去一个四棱柱所得的组合体，
圆柱的底面半径为2，棱柱的底面棱长为2，
两个柱体的高均为4，
故组合体的体积V=（π•22-2×2）×4=16π-16，
故选：A
点评 本题考查的知识点是棱柱的体积和表面积，圆柱的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
1．
阅读如图所示的程序框图，运行相应的程序，输出的结果为（ ）
阅读如图所示的程序框图，运行相应的程序，输出的结果为（ ）| A． | 18 | B． | 20 | C． | 21 | D． | 24 |
18．设某地若干户家庭的年收入x（单位：万元）和年饮食支出y（单位：万元），调查显示x与y具有线性相关关系，并由调查数据得到y对x的回归直线方程为：$\widehat{y}$=0.254x+0.321．由回归直线方程可知，家庭年收入每增加1万元，则年饮食支出平均增加（ ）
| A． | 0.254万元 | B． | 0.321万元 | C． | 0.575万元 | D． | -0.254万元 |
5．已知集合A={1，2，3，4}，B={1，3，5}，则A∪B等于（ ）
| A． | {1，3} | B． | {1，2，3，4，5} | C． | {2，4} | D． | {1，3，4} |
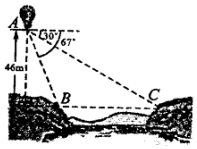如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46m，则河流的宽度BC约等于60m．（用四舍五入法将结果精确到个位．参考数据：sin67°≈0.92，cos67°≈0.39，sin37°≈0.60，cos37°≈0.80，$\sqrt{3}$≈1.73．
2．已知x=1是函数f（x）=ax3-bx-lnx（a＞0，b∈R）的一个极值点，则lna与b-1的大小关系是（ ）
| A． | lna＞b-1 | B． | lna＜b-1 | C． | lna=b-1 | D． | 以上都不对 |