题目内容
设函数f(x)=a2ln x-x2+ax,a>0.
(1)求f(x)的单调区间;
(2)求所有的实数a,使e-1≤f(x)≤e2对x∈[1,e]恒成立.
注:e为自然对数的底数.
解 (1)因为f(x)=a2ln x-x2+ax,其中x>0,
所以
由于a>0,所以f(x)的增区间为(0,a),减区间为(a,+∞).
(2)由题意得f(1)=a-1≥e-1,即a≥e.
由(1)知f(x)在[1,e]内单调递增,
要使e-1≤f(x)≤e2对x∈[1,e]恒成立.
只要 解得a=e.
解得a=e.

练习册系列答案
相关题目
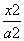 -
- =1(a>0,b>0)的左、右焦点分别为F1、F2,以|F1F2|为直径的圆与双曲
=1(a>0,b>0)的左、右焦点分别为F1、F2,以|F1F2|为直径的圆与双曲 线渐近线的一个交点为(3,4),则此双曲线的方程为( )
线渐近线的一个交点为(3,4),则此双曲线的方程为( )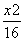 -
- =1 B.
=1 B.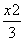 -
-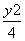 =1
=1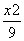 -
-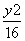 =1 D.
=1 D.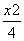 -
-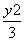 =1
=1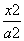 -
-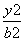 =1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则双曲线C的离心率为________.
=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则双曲线C的离心率为________.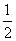 .
.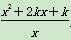 ,对∀x1∈(0,+∞),∃x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
,对∀x1∈(0,+∞),∃x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;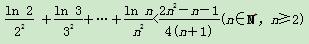 .
.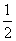 <2x<8,x∈R},B={x|-1<x<m+1,x∈R},若x∈B成立的一个充分不必要的条件是x∈A,则实数m的取值范围是________.
<2x<8,x∈R},B={x|-1<x<m+1,x∈R},若x∈B成立的一个充分不必要的条件是x∈A,则实数m的取值范围是________.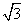 cos(2x+φ)+sin(2x+φ)
cos(2x+φ)+sin(2x+φ)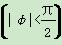 ,且其图象关于直线x=0对称,则( )
,且其图象关于直线x=0对称,则( )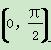 上为增函数
上为增函数 上为增函数
上为增函数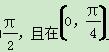 上为减函数
上为减函数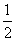 ,其图象的一条对称轴为x=
,其图象的一条对称轴为x= .
.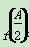 =1,b=1,S△ABC=
=1,b=1,S△ABC= B.
B. C.
C. D.
D.
 ,函数
,函数 ,若
,若 ,且
,且 ,则
,则 的取值范围是
的取值范围是