题目内容
直线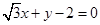 截圆
截圆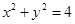 得到的弦长为 .
得到的弦长为 .
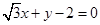 截圆
截圆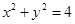 得到的弦长为 .
得到的弦长为 .
试题分析:因为根据圆的方程可知,圆的半径为2,圆心(0,0)到直线的距离为d=
 ,
,则利用勾股定理,半弦长和点到直线的距离,和半径的关系得到,∴弦长为 2
 =2
=2 ,故答案为
,故答案为 。
。点评:解决该试题的关键是先求出圆心和半径,求出圆心(0,0)到直线的距离为d,利用弦长公式求出弦长

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
题目内容
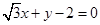 截圆
截圆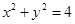 得到的弦长为 .
得到的弦长为 .
 ,
, =2
=2 ,故答案为
,故答案为 。
。
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案