题目内容
若 ,则直线
,则直线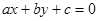 被圆
被圆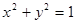 所截得的弦长为( )
所截得的弦长为( )
 ,则直线
,则直线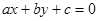 被圆
被圆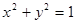 所截得的弦长为( )
所截得的弦长为( ) A. | B.1 | C. | D.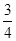 |
B
试题分析:因为
 ,而圆的方程中圆心为原点,半径为1,那么则利用
,而圆的方程中圆心为原点,半径为1,那么则利用点到直线 的距离公式可知
 ,同时达到
,同时达到 ,则
,则可知圆心到直线的距离小于圆的半径1,可知直线与圆相交,且半弦长为
 ,那么可知截得的弦长为1,选B。
,那么可知截得的弦长为1,选B。点评:解决该试题的关键是理解直线与圆的位置关系的判定就是看圆心到直线的距离与圆的
半径的大小关系的运用。

练习册系列答案
相关题目
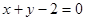 上的圆的方程是 .
上的圆的方程是 .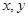 的方程
的方程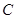 :
: .
. 为何值时,方程C表示圆。
为何值时,方程C表示圆。 相交于M,N两点,且|MN|=
相交于M,N两点,且|MN|= ,求
,求 ,使得圆上有四点到直线
,使得圆上有四点到直线 的距离为
的距离为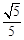 ,若存在,求出
,若存在,求出 的范围,若不存在,说明理由。
的范围,若不存在,说明理由。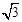 ,求直线l的方程.
,求直线l的方程.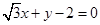 截圆
截圆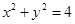 得到的弦长为 .
得到的弦长为 .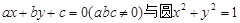 相离,若
相离,若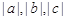 能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________.
能表示为某三角形的三条边长,则根据已知条件能够确定该三角形的形状是____________. 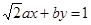 与圆
与圆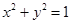 相交于
相交于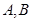 两点(其中
两点(其中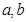 是实数),且
是实数),且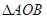 是直角三角形(
是直角三角形(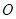 是坐标原点),则点
是坐标原点),则点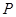
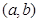 与点
与点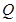
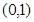 之间距离的最大值为 ( )
之间距离的最大值为 ( )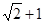
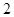

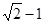
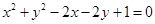 上的点到直线
上的点到直线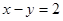 的距离的最大值是
的距离的最大值是