题目内容
已知函数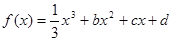 ,设曲线
,设曲线 在与
在与 轴交点处的切线为
轴交点处的切线为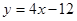 ,
,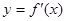 为
为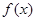 的导函数,满足
的导函数,满足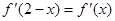 .
.
(1)求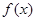 ;
;
(2)设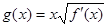 ,
,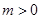 ,求函数
,求函数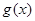 在
在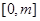 上的最大值;
上的最大值;
(3)设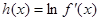 ,若对于一切
,若对于一切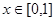 ,不等式
,不等式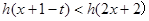 恒成立,求实数
恒成立,求实数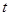 的取值范围.
的取值范围.
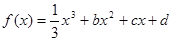 ,设曲线
,设曲线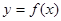 在与
在与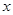 轴交点处的切线为
轴交点处的切线为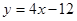 ,
,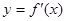 为
为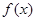 的导函数,满足
的导函数,满足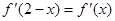 .
.(1)求
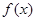 ;
;(2)设
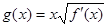 ,
,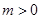 ,求函数
,求函数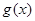 在
在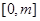 上的最大值;
上的最大值;(3)设
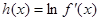 ,若对于一切
,若对于一切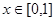 ,不等式
,不等式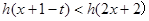 恒成立,求实数
恒成立,求实数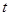 的取值范围.
的取值范围.(1)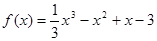 ;(2)
;(2)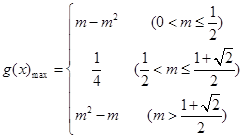 ;(3)
;(3)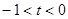 .
.
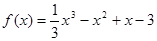 ;(2)
;(2)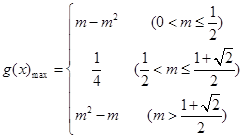 ;(3)
;(3)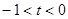 .
.试题分析:(1)三次函数的导数是二次函数,由
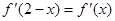 ,知其对称轴,曲线的切线问题,可利用导数的几何意义(切点处切线的斜率)列出方程组求解;(2)
,知其对称轴,曲线的切线问题,可利用导数的几何意义(切点处切线的斜率)列出方程组求解;(2)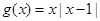 ,画出函数图象考察其单调性,根据其单调区间对
,画出函数图象考察其单调性,根据其单调区间对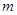 的值分类讨论求出其最大值;(3)对不等式
的值分类讨论求出其最大值;(3)对不等式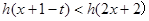 进行化简,得
进行化简,得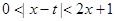 恒成立,即
恒成立,即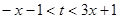 ,且
,且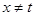 ,对任意的
,对任意的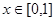 成立,然后又转化为求函数的最值问题,要注意
成立,然后又转化为求函数的最值问题,要注意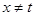 ,从而有
,从而有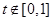 .
.试题解析:(1)
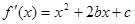 ,∵
,∵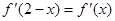 ,
,∴函数
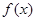 的图象关于直线
的图象关于直线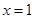 对称,
对称,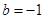 , 2分
, 2分∵曲线
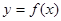 在与
在与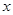 轴交点处的切线为
轴交点处的切线为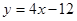 ,∴切点为
,∴切点为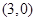 ,
,∴
 ,解得
,解得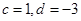 ,则
,则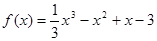 5分
5分(2)∵
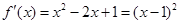 ,
,∴
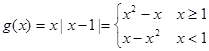 ,其图象如图 7分
,其图象如图 7分当
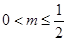 时,
时, ,
,当
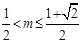 时,
时,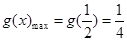 ,
,当
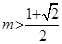 时,
时,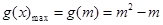 ,
,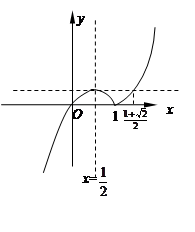
综上
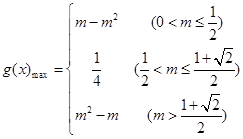 10分
10分(3)
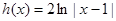 ,
,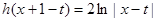 ,
,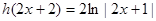
当
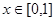 时,
时,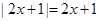 ,所以不等式等价于
,所以不等式等价于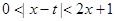 恒成立,
恒成立,解得
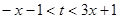 ,且
,且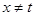 , 13分
, 13分由
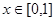 ,得
,得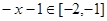 ,
,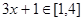 ,所以
,所以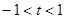 ,
,又
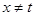 ,∵
,∵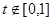 ,∴所求的实数
,∴所求的实数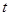 的的取值范围是
的的取值范围是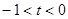 16分
16分
练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
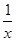 -a
-a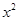 +x(a>0).
+x(a>0).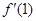 =
=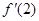 ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程;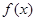 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: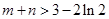 .
.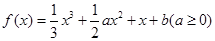 ,
,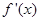 为函数
为函数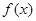 的导函数.
的导函数. 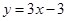 ,求
,求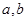 的值;
的值;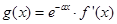 ,求函数
,求函数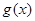 的单调区间.
的单调区间.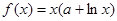 有极小值
有极小值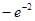 .
.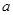 的值;
的值;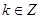 ,且
,且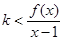 对任意
对任意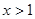 恒成立,求
恒成立,求 的最大值为.
的最大值为.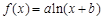 ,
,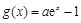 (其中
(其中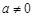 ,
,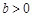 ),且函数
),且函数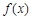 的图象在点
的图象在点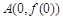 处的切线与函数
处的切线与函数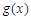 的图象在点
的图象在点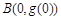 处的切线重合.
处的切线重合.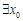 ,满足
,满足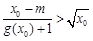 ,求实数
,求实数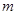 的取值范围;
的取值范围;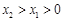 ,试探究
,试探究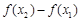 与
与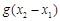 的大小,并说明你的理由.
的大小,并说明你的理由.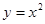 在
在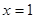 处的切线与两坐标轴围成三角形区域为
处的切线与两坐标轴围成三角形区域为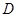 (包含三角形内部与边界).若点
(包含三角形内部与边界).若点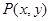 是区域
是区域 的取值范围是__________.
的取值范围是__________.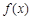 的图像如图所示,则不等式
的图像如图所示,则不等式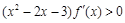 的解集为( )
的解集为( )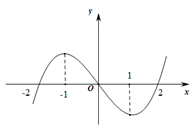




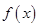 的导函数为
的导函数为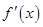 ,且满足关系式
,且满足关系式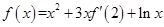 ,则
,则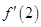 的值等于( )
的值等于( )


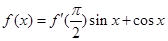 ,则
,则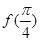 = .
= .