题目内容
已知函数f(x)=ln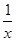 -a
-a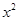 +x(a>0).
+x(a>0).
(Ⅰ)若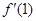 =
=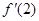 ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程;
(Ⅱ)若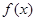 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: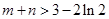 .
.
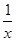 -a
-a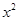 +x(a>0).
+x(a>0).(Ⅰ)若
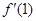 =
=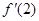 ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程;(Ⅱ)若
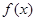 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: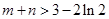 .
.(Ⅰ)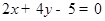 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
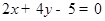 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.试题分析:(Ⅰ)若
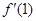 =
=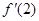 ,求
,求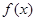 图像在
图像在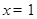 处的切线的方程,须求
处的切线的方程,须求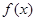 图像在
图像在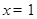 处的切线的斜率,即
处的切线的斜率,即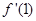 的值,及
的值,及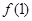 的值,这样需求参数
的值,这样需求参数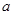 的值,注意到条件
的值,注意到条件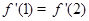 ,可以建立方程来确定参数
,可以建立方程来确定参数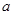 的值,本题思维简单,学生比较容易得分;(Ⅱ)证明:
的值,本题思维简单,学生比较容易得分;(Ⅱ)证明: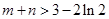 ,需要求出
,需要求出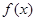 的极大值和极小值,但此题是字母,不能求出,可考虑它们的和的问题,可设极大值点,与极小值点分别为
的极大值和极小值,但此题是字母,不能求出,可考虑它们的和的问题,可设极大值点,与极小值点分别为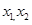 ,利用根与系数关系,得
,利用根与系数关系,得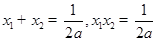 ,这样
,这样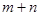 就转化为关于参数
就转化为关于参数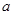 的关系式,利用导数求出
的关系式,利用导数求出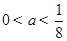 的单调性,从而证出,此题出题新颖,构思巧妙,确实是一个好题.
的单调性,从而证出,此题出题新颖,构思巧妙,确实是一个好题.试题解析:(Ⅰ)

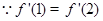 ,
,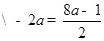 ,即
,即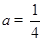
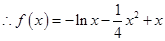 ,
,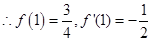 ,
,
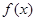 图像在
图像在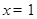 处的切线的方程为
处的切线的方程为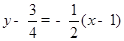 ,即
,即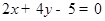 ;
;(Ⅱ)设
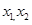 为方程
为方程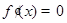 的两个实数根,则
的两个实数根,则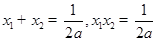 ,由题意得:
,由题意得: 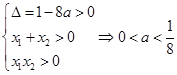 ,
, ,
,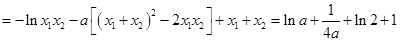 ,令
,令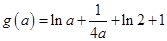 ,则
,则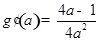 ,
,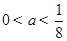 时,
时,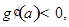
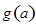 是减函数,则
是减函数,则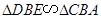
即
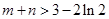 .
.
练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
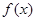
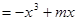 在
在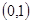 上是增函数,
上是增函数,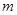 的取值集合
的取值集合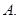 ;
;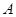 中的最小值时,定义数列
中的最小值时,定义数列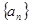 ;满足
;满足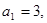 且
且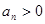 ,
,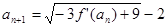 ,求数列
,求数列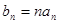 ,数列
,数列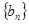 的前
的前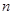 项和为
项和为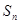 ,求证:
,求证: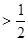 .
. .
. 在区间
在区间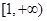 上是单调函数,求
上是单调函数,求 的取值范围;
的取值范围;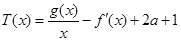 在区间
在区间 内有两个不同的零点(
内有两个不同的零点( 是自然对数的底数)?若存在,求出实数
是自然对数的底数)?若存在,求出实数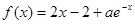 (
(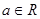 )
)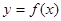 在点
在点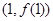 处的切线平行于
处的切线平行于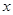 轴,求
轴,求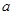 的值;
的值;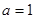 时,若直线
时,若直线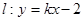 与曲线
与曲线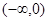 上有公共点,求
上有公共点,求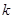 的取值范围.
的取值范围. ,(
,( )在
)在 处取得最小值.
处取得最小值. 的值;
的值; 在
在 处的切线方程为
处的切线方程为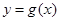 ,求证:当
,求证:当 时,曲线
时,曲线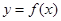 不可能在直线
不可能在直线 ,(
,( )且
)且 ,试比较
,试比较 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.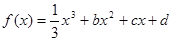 ,设曲线
,设曲线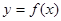 在与
在与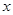 轴交点处的切线为
轴交点处的切线为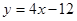 ,
,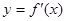 为
为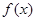 的导函数,满足
的导函数,满足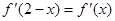 .
.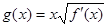 ,
,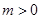 ,求函数
,求函数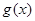 在
在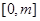 上的最大值;
上的最大值;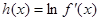 ,若对于一切
,若对于一切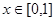 ,不等式
,不等式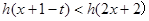 恒成立,求实数
恒成立,求实数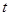 的取值范围.
的取值范围.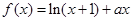 (
(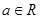 且
且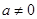 )
)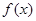 的单调性;
的单调性;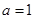 ,证明:
,证明: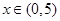 时,
时,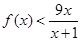 成立
成立 (
( ).
).  时,求函数
时,求函数 的单调区间;
的单调区间; 时,
时,
 上的最小值;
上的最小值;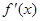 ,当
,当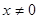 时,
时,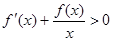 ,若
,若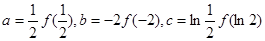 ,则下列关于a,b,c的大小关系正确的是( )
,则下列关于a,b,c的大小关系正确的是( )