题目内容
20．已知{an}是等差数列，公差为2，则a5-a2=6．分析 利用等差数列的通项公式求解．
解答 解：∵{an}是等差数列，公差为2，
∴a5-a2=（a1+4d）-（a1+d）=3d=6．
故答案为：6．
点评 本题考查等差数列的两项差的求法，是基础题，解题时要认真审题，注意等差数列的通项公式的合理运用．
练习册系列答案
相关题目
10．
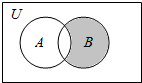设全集U是自然数集N，集合A={x|x2＞4，x∈N}，B={0，2，3}，则图中阴影部分所表示的集合是（ ）
设全集U是自然数集N，集合A={x|x2＞4，x∈N}，B={0，2，3}，则图中阴影部分所表示的集合是（ ）| A． | {x|x＞2，x∈N} | B． | {x|x≤2，x∈N} | C． | {0，2} | D． | {1，2} |
11．在△ABC中，角A，B，C所对的边分别为a，b，c．若角A，B，C成等差数列，边a，b，c成等比数列，则sinA•sinC的值为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{{\sqrt{3}}}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
15．已知{an}是等差数列，且a5+a6=12，则a2+a9=（ ）
| A． | 10 | B． | 12 | C． | 20 | D． | 16 |
9．函数y=log3（3-x）的定义域为（ ）
| A． | （-∞，3] | B． | （-∞，3） | C． | （3，+∞） | D． | [3，+∞） |