题目内容
1.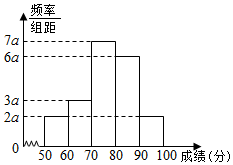 在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:
在一次数学竞赛的200名学生考试成绩中利用随机抽样的方法抽取20名学生考试成绩(单位:分)为样本得频率分布直方图如图:(1)求频率分布直方中a的值;
(2)若60为及格,90分以上(包括90分)为优秀,求这次竞赛不及格率和不及格的学生数以及优秀率和优秀的学生数;
(3)从样本成绩在[50,70)的学生中任选2人,求此2人的成绩都在[60,70)中的概率.
分析 (1)由频率分布直方图的性质得(2a+3a+6a+7a+2a)×10=200a=1,由此能求出a.
(2)先求出分数在60分以下的频率,从而求出这次竞赛不及格的学生人数,求出分数在90分(包括90分)以上的频率,从而能求出这次竞赛优秀的学生人数.
(3)样本中落在[60,70)中的学生人数为3人.设样本中落在[50,60)中的2人成绩为A1,A2,落在[60,70)中的3人为B1,B2,B3.由此能求出此2人的成绩都在[60,70)中的概率.
解答 解:(1)∵组距为10,∴(2a+3a+6a+7a+2a)×10=200a=1,
∴a=$\frac{1}{200}$=0.005.…(2分)
(2)分数在6(0分)以下的频率为2a×10=20a=0.1=10%,
∴这次竞赛不及格的学生人数为0.1×200=20.…(4分)
分数在9(0分)(包括90分)以上的频率为2a×10=20a=0.1=10%,
∴这次竞赛优秀的学生人数为0.1×200=20.…(6分)
(3)∵样本中落在[60,70)中的学生人数为3a×10×20=3×0.005×10×20=3.
∴设样本中落在[50,60)中的2人成绩为A1,A2,落在[60,70)中的3人为B1,B2,B3.
则从[50,70)中选2人共有$C_5^2=\frac{5×4}{2}=10$种选法,
其中2人都在[60,70)中的基本事件有$C_3^2=C_3^1=3$种,
故所求概率p=$\frac{3}{10}$.…(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
9.已知角α的终边过点P(-8m,-6sin150°),且cosα=-$\frac{4}{5}$,则m的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
16.已知O为坐标原点,点P的坐标(x,y)满足约束条件$\left\{\begin{array}{l}{x+|y|≤1}\\{x≥0}\end{array}\right.$,则z=y-ax取得最大(小)值的最优解不唯一,则实数a的值为( )
| A. | $\frac{1}{2}$或-1 | B. | 2或-1 | C. | 2或1 | D. | 1或-1 |
6.若x∈{1,2,3},y∈{3,6},则xy的不同值有( )
| A. | 3个 | B. | 5个 | C. | 6个 | D. | 9个 |
13.一个均匀的正方体玩具的各个面上分别标有数字1,2,3,4,5,6,将这个玩具向上抛掷一次,设事件A表示向上的一面出现奇数点,事件B表示向上的一面出现的点数不超过2,事件C表示向上的一面出现的点数不小于4,则( )
| A. | A与B是互斥而非对立事件 | B. | A与B是对立事件 | ||
| C. | B与C是互斥而非对立事件 | D. | B与C是对立事件 |
10.已知f(c)=(c-a)(c-b),其中a+b=1-c且c≥0,a≥0,b≥0.则f(c)的取值范围为( )
| A. | [-$\frac{1}{8}$,1] | B. | [0,1] | C. | [0,$\frac{1}{4}$] | D. | [-$\frac{1}{9}$,1] |