题目内容
如果数列{an}的前n项和为
，那么这个数列的通项公式为
- A.an=2（n2+n+1）
- B.an=3×2n
- C.an=3n+1
- D.an=2×3n
D
分析：利用数列中an与 Sn关系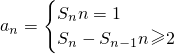
，得出
，且a1=6，由此判定数列为等比数列，通项公式可求．
解答：当n=1时，
，解得a1=6．当n≥2时，an=Sn-S n-1=
，化简整理，
所以数列{an}是以6为首项，以3为公比的等比数列．通项公式an=6×3 n-1=2×3 n．
故选D．
点评：本题考查利用数列中an与 Sn关系求数列通项，考查等比数列判定，通项公式求解．需具有转化、变形、计算能力．
分析：利用数列中an与 Sn关系
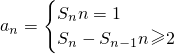，得出，且a1=6，由此判定数列为等比数列，通项公式可求．解答：当n=1时，
，解得a1=6．当n≥2时，an=Sn-S n-1=，化简整理，所以数列{an}是以6为首项，以3为公比的等比数列．通项公式an=6×3 n-1=2×3 n．
故选D．
点评：本题考查利用数列中an与 Sn关系求数列通项，考查等比数列判定，通项公式求解．需具有转化、变形、计算能力．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
如果数列{an}的前n项和Sn=2n-1，那么这个数列（ ）
| A、是等差数列但不是等比数列 | B、是等比数列但不是等差数列 | C、既是等差数列又是等比数列 | D、既不是等差数列又不是等比数列 |