题目内容

已知a1b1+a2b2＞0，且a1，a2，b1，b2都是实数，求证：a1b1+a2b2≤
a
2
1
+
a
2
2
•
b
2
1
+
b
2
2
．
考点：二维形式的柯西不等式
专题：证明题,不等式的解法及应用
分析：利用作差比较法，即可得出结论．
解答： 证明：∵（a12+a22）（b12+b22）-（a1b1+a2b2）2 =a12 b22+a22 b12-2a1b1a2b2=（a1b2-a2b1）2≥0，
∴（a12+a22）（b12+b22）≥（a1b1+a2b2）2成立，
∵a1b1+a2b2＞0，
∴a1b1+a2b2≤
a
2
1
+
a
2
2
•
b
2
1
+
b
2
2
．
点评：本题考查不等式的性质，不等式的证明方法，比较基础．
练习册系列答案
相关题目
“x＞1”是“
1
x
＜1”的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充分必要条件
D、既不充分也不必要条件
已知圆C：（x+1）2+y2=20点B（l，0）．点A是圆C上的动点，线段AB的垂直平分线与线段AC交于点P．
（I）求动点P的轨迹C1的方程；
（Ⅱ）设M(0，
1
5
)，N为抛物线C2：y=x2上的一动点，过点N作抛物线C2的切线交曲线Cl于P，Q两点，求△MPQ面积的最大值．
圆锥的高为h，底面半径为r，过两条母线作一截面，截得底面圆弧的
1
4
，求该截面的面积．
已知函数y=
2x2-ax+1
x2+4x+6
的最小值为1，求实数a的取值范围．
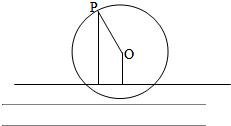如图是一个半径为3米的水轮，水轮圆心O距离水面2米，已知水轮每分钟转动四圈，水轮上的点P相对于水面的高度y（米）与时间x（秒）满足函数关系y=Asin（ωx+φ）+2（A＞0，ω＞0，φ∈（-
π
2
，
π
2
）），且初始位置时y=
7
2
，则函数表达式为
 
．
求f（x）=
1-x2
x+3
的值域．
求证：
5
是无理数．
设函数f（x）=x2，g（x）=alnx+bx（a＞0）．
（1）若f（1）=g（1），f′（1）=g′（1）求F（x）=f（x）-g（x）的极小值；
（2）在（1）的结论下，是否存在实常数k和m，使得f（x）≥kx+m和g（x）≤kx+m同时成立？若存在，求出k和m的值．若不存在，说明理由．
（3）设G（x）=f（x）+2-g（x）有两个零点x1和x2，若x0=
x1+x2
2
，试探究G′（x0）值的符号．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网