题目内容
18.老张身高176cm,他爷爷、父亲、儿子的身高分别是173cm、170cm和182cm,因儿子的身高与父亲的身高有关,父亲的身高用x表示,儿子的身高用y来表示.(1)完成答题卡中的表格;
(2)用回归分析的方法得到的回归方程为$\stackrel{∧}{y}$=bx+$\stackrel{∧}{a}$,则预计老张的孙子的身高为多少?
分析 (1)根据题意,填写关于x、y的表格即可;
(2)由题意计算$\overline{x}$、$\overline{y}$与回归系数,写出回归方程,
利用回归方程预测老张孙子的身高.
解答 解:(1)根据题意,填表如下;
| x | 173 | 170 | 176 |
| y | 170 | 176 | 182 |
(2)由题意,计算$\overline{x}$=$\frac{1}{3}$×(173+170+176)=173,
$\overline{y}$=$\frac{1}{3}$×(170+176+182)=176;…(4分)
$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{0×({-6})+({-3})×0+3×6}}{{{0^2}+{{({-3})}^2}+{3^2}}}=1$,
$\hat a=176-1×173=3$;…(8分)
回归方程为$\stackrel{∧}{y}$=x+3,
由此预计老张的孙子的身高为185 cm.…(10分)
点评 本题考查了线性回归方程的求法与应用问题,是基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
6.一个总体分为A,B,C三层,用分层抽样方法从总体中抽取容量为50的样本,已知B层中每个个体被抽到的概率都为$\frac{1}{12}$,则总体容量为( )
| A. | 150 | B. | 200 | C. | 500 | D. | 600 |
13.已知函数$f(x)=\frac{1}{2}{x^3}+ax-b$在区间[-1,1]上为增函数,则在区间[0,1]上任意取两个实数a,b,使f(x)在区间[-1,1]上有且仅有一个零点的概率为( )
| A. | $\frac{{\sqrt{3}}}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{8}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
3.函数f(x)=x2+2x+1的单调递增区间是( )
| A. | [-1,+∞) | B. | [1,+∞) | C. | (-∞,-1] | D. | (-∞,1] |
7.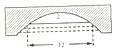 如图,一座圆弧形拱桥,当水面在如图所示的位置时,拱桥离水面2米,水面宽12米,当水面下降1米后,水面宽度为( )
如图,一座圆弧形拱桥,当水面在如图所示的位置时,拱桥离水面2米,水面宽12米,当水面下降1米后,水面宽度为( )
 如图,一座圆弧形拱桥,当水面在如图所示的位置时,拱桥离水面2米,水面宽12米,当水面下降1米后,水面宽度为( )
如图,一座圆弧形拱桥,当水面在如图所示的位置时,拱桥离水面2米,水面宽12米,当水面下降1米后,水面宽度为( )| A. | 14米 | B. | 15米 | C. | $\sqrt{51}$米 | D. | $2\sqrt{51}$ |
8.下列函数中是偶函数的有( )
| A. | y=x2 | B. | y=x | C. | y=x3 | D. | y=2x |