已知相关变量x和$\stackrel{∧}{y}$满足关系$\stackrel{∧}{y}$=-x+1相关变量y与$\stackrel{∧}{z}$满足$\stackrel{∧}{z}$=3y+4.下列结论中正确的( )A．x和$\stackrel{∧}{y}$负相关.y与$\stackrel{∧}{z}$负相关B．x和$\stackrel{∧}{y}$正相关.y与$\stackrel{ 题目和参考答案——青夏教育精英家教网—

题目内容

11．已知相关变量x和$\stackrel{∧}{y}$满足关系$\stackrel{∧}{y}$=-x+1相关变量y与$\stackrel{∧}{z}$满足$\stackrel{∧}{z}$=3y+4，下列结论中正确的（　　）

	A．	x和$\stackrel{∧}{y}$负相关，y与$\stackrel{∧}{z}$负相关		B．	x和$\stackrel{∧}{y}$正相关，y与$\stackrel{∧}{z}$正相关
	C．	x和$\stackrel{∧}{y}$正相关，y与$\stackrel{∧}{z}$负相关		D．	x和$\stackrel{∧}{y}$负相关，y与$\stackrel{∧}{z}$正相关

分析根据回归方程，分析当变量增大时，两个变量之间的变化情况即可．

解答解：相关变量x和$\stackrel{∧}{y}$满足关系$\stackrel{∧}{y}$=-x+1，
∴y随x的增大而减小，x和$\stackrel{∧}{y}$负相关；
相关变量y与$\stackrel{∧}{z}$满足$\stackrel{∧}{z}$=3y+4，
∴z随y的增大而增大，y和$\stackrel{∧}{z}$正相关．
故选：D．

点评本题考查了变量间的相关关系应用问题，是基础题．

练习册系列答案

	A．	向右平移$\frac{π}{12}$个单位		B．	向左平移$\frac{π}{4}$个单位
	C．	向左平移$\frac{π}{12}$个单位		D．	向右平移$\frac{π}{4}$个单位

2．方程$\frac{x^2}{m+2}+\frac{y^2}{m-2}=1$表示双曲线，则m的取值范围是（-2，2）．

19．函数$f（x）={cos^2}（x-\frac{π}{12}）+{sin^2}（x+\frac{π}{12}）-1$是（　　）

	A．	奇函数		B．	偶函数
	C．	既是奇函数又是偶函数		D．	既不是奇函数又不是偶函数

6．

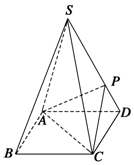如图，四棱锥S-ABCD的底面是正方形，边长为$\sqrt{2}$，每条侧棱的长都是底面边长的$\sqrt{2}$倍，P为侧棱SD上的点．
（1）求证：AC⊥SD；
（2）若SD⊥平面PAC，求CP与平面SBC所成角的正弦值．

16．已知a，b，c＞0，求证$\frac{{{a^2}{b^2}+{b^2}{c^2}+{a^2}{c^2}}}{a+b+c}≥abc$．

3．给出下列结论：
①扇形的圆心角为120°，半径为2，则扇形的弧长是$\frac{4π}{3}$；
②某小礼堂有25排座位，每排20个，一次心理学讲座，礼堂中坐满了学生，会后为了了解有关情况，留下座位号是15的所有25名学生进行测试，这里运用的是系统抽样方法；
③一个人打靶时连续射击两次，则事件“至少有一次中靶”与事件“两次都不中靶”互为对立事件；
④若0＜x＜$\frac{π}{2}$，则tanx＞x＞sinx；
⑤若数据x₁，x₂，…，x_n的方差为8，数据2x₁+1，2x₂+1，…，2x_n+1的方差为16．
其中正确结论的序号为①②③④．（把你认为正确结论的序号都填上）

11．已知函数f（x）=2cosxsin（x+$\frac{π}{6}$）+1，x∈R．
（Ⅰ）求函数f（x）的最小正周期及单调递增区间；
（Ⅱ）将f（x）的图象向右平移$\frac{π}{3}$个单位得到函数g（x）的图象，若x∈[-$\frac{π}{6}$，$\frac{π}{3}$]，求函数g（x）的值域．

12．将除颜色外完全相同的一个白球、一个黄球、两个红球分给三个小朋友，且每个小朋友至少分得一个球的分法有21（种）．

试题分类