题目内容
若函数f(x)=||x-1|-1|的图象与y=m有4个不同的公共点为a,b,c,d,求m的取值范围.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:首先根据函数的表达式画出函数f(x))=||x-1|-1|与y=m的图象,然后根据图象判断函数与直线的公共点的情况,求出m的取值范围即可.
解答:
解:f(x)=||x-1|-1|=
,
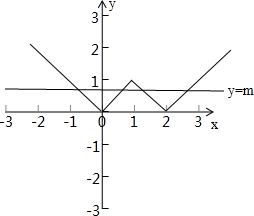
画出函数f(x)=||x-1|-1|与y=m的图象如下,
因为函数f(x)=||x-1|-1|的图象与y=m有4个不同的公共点,
所以根据图象,可得m的取值范围是(0,1).
|
画出函数f(x)=||x-1|-1|与y=m的图象如下,
因为函数f(x)=||x-1|-1|的图象与y=m有4个不同的公共点,
所以根据图象,可得m的取值范围是(0,1).

点评:本题主要考查了函数的图象和性质,以及数形结合方法的运用,属于中档题,数形结合是数学解题中常用的思想方法,它能使使复杂的问题简单化.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=