题目内容
 已知函数f(x)=
已知函数f(x)=| 1 |
| 2 |
| π |
| 4 |
(Ⅰ)求它的振幅、最小正周期、初相;
(Ⅱ)画出函数y=f(x)在[-
| π |
| 2 |
| π |
| 2 |
考点:正弦函数的图象,五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的图像与性质
分析:(Ⅰ)根据振幅、最小正周期、初相的定义求出函数f(x))=
sin(2x+
)+1的振幅、最小正周期、初相.
(Ⅱ)用五点法画出函数y=f(x)在[-
,
]上的图象.
| 1 |
| 2 |
| π |
| 4 |
(Ⅱ)用五点法画出函数y=f(x)在[-
| π |
| 2 |
| π |
| 2 |
解答:
解:(Ⅰ)对于函数f(x)=
sin(2x+
)+1,振幅A=
,最小正周期T=
=π,
初相为
.
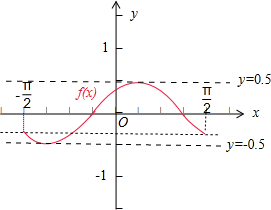
(Ⅱ)用五点法画出函数y=f(x)在[-
,
]上的图象:
由x∈[-
,
],可得 2x+
∈[-
,
],
列表:
画图:
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 2π |
| 2 |
初相为
| π |
| 4 |
(Ⅱ)用五点法画出函数y=f(x)在[-
| π |
| 2 |
| π |
| 2 |
由x∈[-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
列表:
2x+
| -
| -
| 0 |
| π |
| ||||||||||||
| x | -
| -
| -
|
|
| -
| ||||||||||||
| y | -
| -
| 0 |
| 0 | -
|

点评:本题主要考查正弦函数的图象特征,本题主要考查用五点法作函数y=Asin(ωx+φ)在一个周期上的简图,属于基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC.
三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC.