题目内容
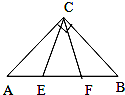
如图，E、F是等腰直角△ABC斜边AB上的三等分点，则tan∠ECF=
考点：两角和与差的正切函数
专题：计算题
分析：由题意及图形，并有等腰直角可以设直角边长为3，则写斜边长为3
，利用E、F是等腰直角△ABC斜边上的三等分点及余弦定理就可求出CE，CF的长度，在△CEF中利用余弦定理求出即可．
| 2 |
解答：
解：由题意及图形：设三角形的直角边为3，则斜边为3
，又由于E，F为三等分点，
所以AE=EF=BF=
，又△ACE≌△BCF，
在△ACE中有余弦定理得：CE2=AC2+AE2-2AC•AEcos45°⇒CE=
=CF，
在△CEF中，利用余弦定理得：cos∠ECF=
=
，
在△ECF中利用同角间的三角函数关系可知：tan∠ECF=
．
故答案为：
．
| 2 |
所以AE=EF=BF=
| 2 |
在△ACE中有余弦定理得：CE2=AC2+AE2-2AC•AEcos45°⇒CE=
| 5 |
在△CEF中，利用余弦定理得：cos∠ECF=
| CF2+CE2-EF2 |
| 2•CF•CE |
| 4 |
| 5 |
在△ECF中利用同角间的三角函数关系可知：tan∠ECF=
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：此题考查了同角三角函数的关系、余弦定理及学生的计算能力，属于中档题．
练习册系列答案
相关题目
求棱长为a的正四面体的内切球和外接球的体积之比为（ ）
| A、1：27 | B、1：9 |
| C、1：3 | D、9：1 |
给出下列四个命题：
①若x2-3x+2=0，则x=1或x=2
②若-2≤x＜3，则（x+2）（x-3）≤0
③若x=y=0，则x2+y2=0
④若x，y∈N*，x+y是奇数，则x，y中一个是奇数，一个是偶数，
那么下列说法正确的是（ ）
①若x2-3x+2=0，则x=1或x=2
②若-2≤x＜3，则（x+2）（x-3）≤0
③若x=y=0，则x2+y2=0
④若x，y∈N*，x+y是奇数，则x，y中一个是奇数，一个是偶数，
那么下列说法正确的是（ ）
| A、①的逆命题为真 |
| B、②的否命题为真 |
| C、③的逆否命题为假 |
| D、④的逆命题为假 |