题目内容

14．已知函数f（x）=ex-ax2-x-1（a∈R）恰有两个极值点x1，x2（其中x1＜x2），且f（x2）=0，则a的取值范围是（　　）
A．$（-∞，\frac{1}{2}）$B．（0，1）C．$（0，\frac{1}{2}）$D．$（\frac{1}{2}，+∞）$

分析 根据题意，对函数f（x）求导数，得出导数f′（x）=0有两不等实根，转化为两函数有两个交点的问题，结合图象即可得出a的取值范围．

解答 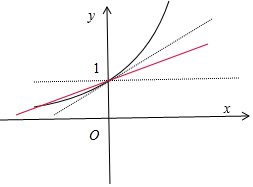解：令g（x）=f′（x）=ex-2ax-1，则方程ex-2ax-1=0有两不等实根，
即直线y=2ax+1与函数y=ex的图象有两个交点，
易得其中一个交点为（0，1），而f（0）=0，∴x1＜0，x2=0，
当直线y=2ax+1与函数y=ex的图象相切于点（0，1）时，2a=e0=1，即$a=\frac{1}{2}$，
故由图象知，a的取值范围是$（0，\frac{1}{2}）$，
故选：C．

点评 本题考查了利用导数研究函数的单调性与极值的应用问题，也考查了转化思想与数形结合的应用问题，是综合性题目．

练习册系列答案
相关题目
4．下列命题中正确的序号是①⑤
①若$\overrightarrow{a}$与$\overrightarrow{b}$为非零向量，且$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\overrightarrow{a}$+$\overrightarrow{b}$必与$\overrightarrow{a}$或$\overrightarrow{b}$的方向相同；
②若$\overrightarrow{e}$为单位向量，且$\overrightarrow{a}$∥$\overrightarrow{e}$，则$\overrightarrow{a}$=|$\overrightarrow{a}$|$\overrightarrow{e}$；
③$\overrightarrow{a}$•$\overrightarrow{a}$•$\overrightarrow{a}$=|$\overrightarrow{a}$|3；
④若$\overrightarrow{a}$与$\overrightarrow{b}$共线，又$\overrightarrow{b}$与$\overrightarrow{c}$共线，则$\overrightarrow{a}$与$\overrightarrow{c}$必共线；
⑤若平面内有四点A，B，C，D，则必有$\overrightarrow{AC}$+$\overrightarrow{BD}$=$\overrightarrow{BC}$+$\overrightarrow{AD}$．
5．设x，y满足约束条件：$\left\{\begin{array}{l}{x，y≥0}\\{x-y≥-1}\\{x+y≤3}\end{array}\right.$，则z=x-2y的最大值为3．
2．已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，且（$\overrightarrow{a}$+2$\overrightarrow{b}$）•（$\overrightarrow{a}$$-\overrightarrow{b}$）=-2，则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为π．
9．若m=2x2+2x+1，n=（x+1）2，则m，n的大小关系为（　　）
A．m＞nB．m≥nC．m＜nD．m≤n
19．已知函数f（x）=Asin（wx+φ）+B（A＞0，w＞），|φ|＜$\frac{π}{2}$） 的部分图象如图所示：
（1）求f（x）的解析式和对称中心坐标；
（2）将f（x）的图象向左平移$\frac{π}{6}$个单位，再将横坐标伸长到原来的2倍，纵坐标不变，最后将图象向上平移1个单位，得到函数g（x）的图象，求函数y=g（x）在x∈[0，$\frac{7π}{6}$]上的最大值和最小值．
6．（在复数范围内）解方程|z|+（z+$\overline{z}$）i=$\frac{3-i}{2+i}$，求解复数z．
3．已知函数f（x）=ex-ax有两个零点x1＜x2，则下列说法正确的个数是（　　）
①a＞e；②x1+x2＞2；③x1x2＞1；④函数f（x）有极小值点x0，x1+x2＜2x0．
A．1B．2C．3D．4
4．若[x]表示不超过x的最大整数，则图中的程序框图运行之后输出的结果为（　　）
A．400B．600C．10D．15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网