题目内容
7．求：$\frac{{sin330°•tan（-\frac{13}{3}π）}}{{cos（-\frac{19}{6}π）•cos690°}}$的值．分析 利用三角函数的诱导公式分别化简各因式即可；注意符号．
解答 解：原式=$\frac{sin（360°-30°）tan（-4π-\frac{π}{3}）}{cos（-3π-\frac{π}{6}）cos（4×180°-30°）}$
=$\frac{-sin30°（-tan\frac{π}{3}）}{-cos\frac{π}{6}cos30°}$
=$\frac{\frac{1}{2}×\sqrt{3}}{-\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}}=-\frac{2\sqrt{3}}{3}$．
点评 本题考查了三角函数的化简求值；属于基础题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
18．已知整数对的序列为（1，1），（1，2），（2，1），（1，3），（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），（1，5），（2，4），…，则第57个数对是（ ）
| A． | （2，10） | B． | （10，2） | C． | （3，5） | D． | （5，3） |
15．如图所示，在△ABC中，点D、E、F分别是边AB、BC、AC的中点，则下面结论正确的是（ ）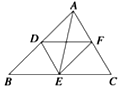
| A． | $\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{FA}$ | B． | $\overrightarrow{DE}+\overrightarrow{AF}=0$ | C． | $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}≠0$ | D． | $\overrightarrow{DE}-\overrightarrow{DF}=\overrightarrow{AD}$ |
17．设f（x）=10x+lgx，则f′（1）等于（ ）
| A． | 10 | B． | 10ln10+$\frac{1}{ln10}$ | C． | $\frac{10}{ln10}$+ln10 | D． | 11ln10 |