题目内容
16.若二次函数f(x)=ax2+bx+c(a,b∈R)满足f(x+1)-f(x)=2x,且f(0)=1.(1)求f(x)的解析式;
(2)若在区间[-1,-1]上,不等式f(x)≥2x+m恒成立,求实数m的取值范围.
分析 (1)由二次函数可设f(x)=ax2+bx+c(a≠0),由f(0)=1求得c的值,由f(x+1)-f(x)=2x可得a,b的值,即可得f(x)的解析式;
(2)欲使在区间[-1,1]上不等式f(x)≥2x+m恒成立,只须x2-3x+1-m≥0在区间[-1,1]上恒成立,也就是要x2-3x+1-m的最小值大于等于0,即可得m的取值范围.
解答 解:(1)由题意可知,f(0)=1,解得,c=1,
由f(x+1)-f(x)=2x.可知,[a(x+1)2+b(x+1)+1]-(ax2+bx+1)=2x,
化简得,2ax+a+b=2x,
∴$\left\{\begin{array}{l}{2a=2}\\{a+b=0}\end{array}\right.$,
∴a=1,b=-1.
∴f(x)=x2-x+1;
(2)不等式f(x)≥2x+m,可化简为x2-x+1≥2x+m,
即x2-3x+1-m≥0在区间[-1,1]上恒成立,
设g(x)=x2-3x+1-m,则其对称轴为x=$\frac{3}{2}$,
∴g(x)在[-1,1]上是单调递减函数.
因此只需g(x)的最小值大于零即可,
g(x)min=g(1),
∴g(1)≥0,
即1-3+1-m≥0,解得,m≤-1,
∴实数m的取值范围是m≤-1.
点评 本题主要考查了利用待定系数法求解二次函数的解析式,以及函数的恒成立与函数的最值求解的相互转化,主要涉及单调性在函数的最值求解中的应用.属于中档题.

练习册系列答案
相关题目
4.P为椭圆$\frac{x^2}{{2{b^2}}}+\frac{y^2}{b^2}=1({b>0})$上异于左右顶点A1、A2的任意一点,则直线PA1与PA2的斜率之积为定值$-\frac{1}{2}$.将这个结论类比到双曲线,得出的结论为:P为双曲线$\frac{x^2}{{2{b^2}}}-\frac{y^2}{b^2}=1({b>0})$上异于左右顶点A1、A2的任意一点,则( )
| A. | 直线PA1与PA2的斜率之和为定值$\frac{1}{2}$ | B. | 直线PA1与PA2的斜率之和为定值2 | ||
| C. | 直线PA1与PA2的斜率之积为定值$\frac{1}{2}$ | D. | 直线PA1与PA2的斜率之积为定值2 |
1.将4本不同的书全部分给3个学生,每个学生至少一本,则不同的分法种数( )种.
| A. | 12 | B. | 36 | C. | 72 | D. | 108 |
5.若关于x不等式xlnx-x3+x2≤aex恒成立,则实数a的取值范围是( )
| A. | [e,+∞) | B. | [0,+∞) | C. | $[\frac{1}{e},+∞)$ | D. | [1,+∞) |
6.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为80秒.若一名行人来到该路口遇到红灯,则至少需要等待30秒才出现绿灯的概率为( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{5}$ |
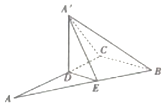 如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.
如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.