题目内容
我省某房地产开发商用2016万元购得一块商业用地，计划在此地上建造一栋至少6层、每层2016平方米的楼房．经测算，如果将楼房建造x层，则每平方米的平均建造费用为（2016+100x）元，为了使楼房每平方米平均的综合费用最小，此楼房应建造多少层？
考点：基本不等式在最值问题中的应用
专题：应用题,不等式的解法及应用
分析：设楼房应建为x层，楼房每平方米的平均综合费为y元，根据平均综合费用=平均建筑费用+平均购地费用，列出函数关系式，然后运用配方法求出函数的最小值，并求出此时x的取值即可．
解答：
解：设楼房应建为x层（x≥6），楼房每平方米的平均综合费为y元，
则y=（2016+100x）+
=2016+100x+
≥2016+2
=4016，
当且仅当
=100x，即x=10时，y取最小值4016．
答：为了楼房每平方米的平均综合费最少，该楼房应建为10层．
则y=（2016+100x）+
| 2016×10000 |
| 2016x |
| 10000 |
| x |
≥2016+2
100x•
|
当且仅当
| 10000 |
| x |
答：为了楼房每平方米的平均综合费最少，该楼房应建为10层．
点评：函数的实际应用题，我们要经过析题→建模→解模→还原四个过程，在建模时要注意实际情况对自变量x取值范围的限制，解模时也要实际问题实际考虑．将实际的最大（小）化问题，利用函数模型，转化为求函数的最大（小）是最优化问题中，最常见的思路之一．
练习册系列答案
相关题目
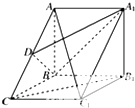如图所示，在三棱柱ABC-A1B1C1中，侧面A1ABB1和BCC1B1是两个全等的正方形，AC1⊥平面A1DB，D为AC的中点．