题目内容
求函数y=(4-3sinx)(4-3cosx)的最小值.
考点:三角函数的最值
专题:三角函数的求值
分析:利用多项式乘以多项式展开,然后令t=sinx+cosx换元,化为关于t的二次函数求最值.
解答:
解:y=(4-3sinx)(4-3cosx)
=16-12(sinx+cosx)+9sinxcosx.
令t=sinx+cosx=
sin(x+
)∈[-
,
],
则t2=1+2sinxcosx,sinxcosx=
.
∴y=16-12(sinx+cosx)+9sinxcosx
=16-12t+
-
=
(9t2-24t+23),t∈[-
,
].
当t=
=
时,y有最小值为
.
=16-12(sinx+cosx)+9sinxcosx.
令t=sinx+cosx=
| 2 |
| π |
| 4 |
| 2 |
| 2 |
则t2=1+2sinxcosx,sinxcosx=
| t2-1 |
| 2 |
∴y=16-12(sinx+cosx)+9sinxcosx
=16-12t+
| 9t2 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
当t=
| 12 |
| 9 |
| 4 |
| 3 |
| 7 |
| 2 |
点评:本题考查了三角函数的最值得求法,考查了换元法,训练了二次函数最值的求法,是中档题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
数列{an}的前n项和Sn=n2-2n-1,则a3+a17=( )
| A、15 | B、17 | C、34 | D、398 |
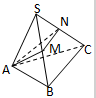 如图,△ABC外一点S,且SA⊥平面ABC,∠ABC=90°,AM⊥SB,AN⊥SC
如图,△ABC外一点S,且SA⊥平面ABC,∠ABC=90°,AM⊥SB,AN⊥SC