题目内容

函数y=tan(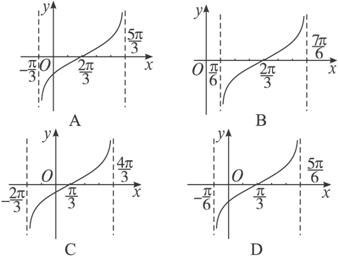x-)在一个周期内的图象是（    ）

解法一:由y=tan(x-)的周期T==2π,而由B、D图象可知周期为π,故可排除B、D.

当x=时,y=tan(-)=-tan≠0,故可排除C,因此应选A.

解法二:∵y=tan(x-)=tan (x-),

∴此函数图象可由y=tanx的图象向右平移个单位得到.而y=tanx的图象过原点,故原函数的图象过点(,0).函数y=tanx的两条渐近线方程x=-π和x=π分别变为x=-和x=,故选A.

答案:A

练习册系列答案
相关题目
函数y=tan(x+
π4
)的定义域为
 
．
给出下列命题：
①若
a
≠
0
，则“
a
•
b
=
a
•
c
”是“
b
=
c
”成立的必要不充分条件
②若
a
=(3，4)，
b
=(0，-1)，则
a
在
b
方向上的投影是-4
③函数y=tan(x+
π
3
)的图象关于点(
π
6
，0)成中心对称
④“一个棱柱的各侧面是全等的矩形”是“这个棱柱是正棱柱”的充要条件
其中真命题是
 
．
下列命题为真命题的是（　　）
函数y=tan(x+
π
3
)的图象的对称中心的坐标是（　　）
A、(kπ-
π
3
，0)，k∈Z
B、(
kπ
2
-
π
3
，0)，k∈Z
C、(
kπ
2
，0)，k∈Z
D、（kπ，0），k∈Z
（2012•株洲模拟）已知函数y=tanωx（ω＞0）的图象与直线y=a相交于A，B两点，若AB长度的最小值为π，则ω的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网