题目内容
15.设α、β、γ是三个不同的平面,a、b是两条不同的直线,下列四个命题中正确的是( )| A. | 若a∥α,b∥α,则a∥b | |
| B. | 若a⊥α,b⊥β,a⊥b,则α⊥β | |
| C. | 若a∥α,b∥β,a∥b,则α∥β | |
| D. | 若a,b在平面α内的射影互相垂直,则a⊥b |
分析 在A中,a与b相交、平行或异面;在B中,由面面垂直的判定定理得α⊥β;在C中,α与β相交或平行;在D中,a与b相交、平行或异面.
解答 解:由α、β、γ是三个不同的平面,a、b是两条不同的直线,知:
在A中,若a∥α,b∥α,则a与b相交、平行或异面,故A错误;
在B中,若a⊥α,b⊥β,a⊥b,则由面面垂直的判定定理得α⊥β,故B正确;
在C中,若a∥α,b∥β,a∥b,则α与β相交或平行,故C错误;
在D中,若a,b在平面α内的射影互相垂直,则a与b相交、平行或异面,故D错误.
故选:B.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列表格所示的五个散点,原本数据完整,且利用最小二乘法求得这五个散点的线性回归直线方程为$\widehaty$=0.8x-155,后因某未知原因第5组数据的y值模糊不清,此位置数据记为m(如表所示),则利用回归方程可求得实数m的值为( )
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
| A. | 8.3 | B. | 8.2 | C. | 8.1 | D. | 8 |
20.下面的各图中,散点图与相关系数r不符合的是( )
| A. | 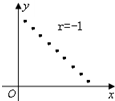 | B. | 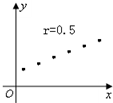 | C. | 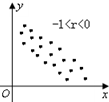 | D. | 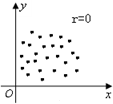 |
7. 如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )
如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )
 如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )
如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )| A. | “合情推理”的下位 | B. | “演绎推理”的下位 | ||
| C. | “直接证明”的下位 | D. | “间接证明”的下位 |
4.已知函数$f(x)=\left\{\begin{array}{l}{log_2}x,x>0\\ sin\frac{π}{6}x,x≤0\end{array}\right.$,则$f[{f(\frac{1}{4})}]$=( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
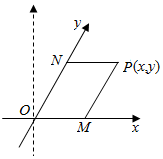 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M,N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为x2+y2+xy-1=0.