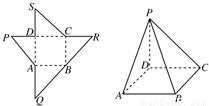
题目内容
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则该几何体的内切球的半径为______.

把该几何体沿图中虚线将其折叠,使P,Q,R,S四点重合,所得几何体为下图中的四棱锥,
且底面四边形ABCD为边长是6的正方形,侧棱PD⊥平面ABCD,PD=6
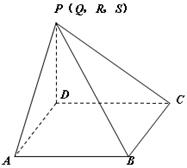
又在折叠前后∠QAB与∠RCB的大小不变,所以四棱锥中∠PAB与∠PCB仍为直角.
在直角三角形PDA和直角三角形PDC中,由PD=DA=DC=6,得PA=PC=6
,
所以S△PDA=S△PDC=
×6×6=18,
S△PAB=S△PCB=
×6×6
=18
,
SABCD=6×6=36.
利用等积法,设四棱锥内切球的半径为r,
则
SABCD•PD=
(S△PAD+SPCD+S△PAB+S△PCB)•r+
SABCD•r.
即36×6=(18×2+18
×2+36)r.
解得:r=6-3
.
故答案为6-3
.
且底面四边形ABCD为边长是6的正方形,侧棱PD⊥平面ABCD,PD=6

又在折叠前后∠QAB与∠RCB的大小不变,所以四棱锥中∠PAB与∠PCB仍为直角.
在直角三角形PDA和直角三角形PDC中,由PD=DA=DC=6,得PA=PC=6
| 2 |
所以S△PDA=S△PDC=
| 1 |
| 2 |
S△PAB=S△PCB=
| 1 |
| 2 |
| 2 |
| 2 |
SABCD=6×6=36.
利用等积法,设四棱锥内切球的半径为r,
则
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
即36×6=(18×2+18
| 2 |
解得:r=6-3
| 2 |
故答案为6-3
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
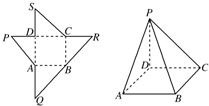 如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要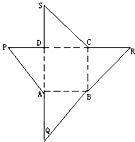 如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则该几何体的内切球的半径为
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则该几何体的内切球的半径为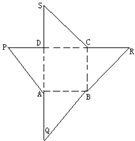 如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠,使P,Q,R,S四点重合,则需要
如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠,使P,Q,R,S四点重合,则需要